Sensitivity analysis and design optimization

Author: Anne Disabato, Tim Hanrahan, Brian Merkle

Steward: David Chen, Fengqi You

Date Presented: February 23, 2014

Introduction

Optimization and sensitivity analysis are key aspects of successful process design. Optimizing a process maximizes project value and plant performance, minimizes project cost, and facilitates the selection of the best components [1].

Design Optimization

Economic optimization is the process of finding the condition that maximizes financial return or, conversely, minimizes expenses. The factors affecting the economic performance of the design include the types of processing technique and equipment used, arrangement, and sequencing of the processing equipment, and the actual physical parameters for the equipment. The operating conditions are also of prime concern.

Optimization of process design follows the general outline below:

1. Establish optimization criteria: using an objective function that is an economic performance measure.
2. Define optimization problem: establish various mathematical relations and limitations that describe the aspects of the design
3. Design a process model with appropriate cost and economic data

Although profitability or cost is generally the basis for optimization, practical and intangible factors usually need to be included as well in the final investment decision. Such factors are often difficult or impossible to quantify, and so decision maker judgment must weigh such factors in the final analysis [3], [4].

Defining the Optimization Problem and Objective Function

In optimization, we seek to maximize or minimize a quantity called the goodness of design or objective function, which can be written as a mathematical function of a finite number of variables called the decision variables.

$z=f(x_{1},x_{2},...x_{n})$

The decision variables may be independent or they may be related via constraint equations. Examples of process variables include operating conditions such as temperature and pressure, and equipment specifications such as the number of trays in a distillation column. The conventional name and strategy of this optimization method varies between texts; Turton suggests creating a base case prior to defining the objective function and Seider classifies the objective function as a piece of a nonlinear program (NLP) [5], [6].

A second type of process variable is the dependent variable; a group of variables influenced by process constraints. Common examples of process constraints include process operability limits, reaction chemical species dependence, and product purity and production rate. Towler & Sinnott define equality and inequality constraints [2]. Equality constraints are the laws of physics and chemistry, design equations, and mass/energy balances:

$h(x_{1},x_{2},...x_{n})=b_{1}$

For example, a distillation column that is modeled with stages assumed to be in phase equilibrium often has several hundred MESH (material balance, equilibrium, summation of mole fractions, and heat balance) equations. However, in the implementation of most simulators, these equations are solved for each process unit, given equipment parameters and steam variables. Hence, when using these simulators, the equality constraints for the process units are not shown explicitly in the nonlinear program. Given values for the design variables, the simulators call upon these subroutines to solve the appropriate equations and obtain the unknowns that are needed to perform the optimization [5].

Inequality constraints are technical, safety, and legal limits, economic and current market:

$g(x_{1},x_{2},...x_{n}){\frac {\geq }{\leq }}b_{2}$

Inequality constrains also pertain to equipment; for example, when operating a centrifugal pump, the head developed is inversely related to the throughput. Hence, as the flow rate is varied when optimizing the process, care must be taken to make sure that the required pressure increase does not exceed that available from the pump [5].

It is important that a problem is not under or over-constrained so a possible solution is attainable. A degree-of-freedom (DOF) analysis should be completed to simply the number of process variables, and determine if the system is properly specified.

Trade-Offs

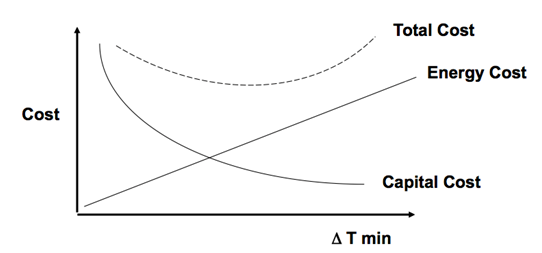
A part of optimization is assessing trade-offs; usually getting better performance from equipment means higher cost. The objective function must capture this trade-off between cost and benefit.

Example: Heat Recovery, total cost captures trade-off between energy savings and capital expense.

Figure 1: Trade-off example [1]

Some common design trade-offs are more separations equipment versus low product purity, more recycle costs versus increased feed use and increased waste, more heat recovery versus cheaper heat exchange system, and marketable by-product versus more plant expense.

Parametric Optimization

Parametric optimization deals with process operating variables and equipment design variables other than those strictly related to structural concerns. Some of the more obvious examples of such decisions are operating conditions, recycle ratios, and steam properties such as flow rates and compositions. Small changes in these conditions or equipment can have a diverse impact on the system, causing parametric optimization problems to contain hundreds of decision variables. It is therefore more efficient to analyze the more influential variables effect on the overall system. Done properly, a balance is struck between increased difficulty of high-variable-number optimization and optimization accuracy. [3]

Suboptimizations

Simultaneous optimization of the many parameters present in a chemical process design can be a daunting task due to the large number of variables that can be present in both integer and continuous form, the non-linearity of the property prediction relationships and performance models, and frequent ubiquity of recycle. It is therefore common to seek out suboptimizations for some of the variables, so as to reduce the dimensionality of the problem [3]. While optimizing sub-problems usually does not lead to overall optimum, there are instances for which it is valid in a practical, economic sense. Care must always be taken to ensure that subcomponents are not optimized at the expense of other parts of the plant.

Equipment optimization is usually treated as a subproblem that is solved after the main process variables such as reactors conversion, recycle ratios, and product recoveries have been optimized.

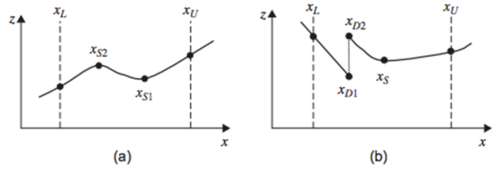
Optimization of a Single Decision Variable

If the objective is a function of a single variable, x, the objective function f(x) can be differentiated with respect to x to give f’(x). The following algorithm summarizes the procedure:

Below is a graphical representation of the above algorithm.

Figure 2. Graphical Illustration of (a) Continuous Objective Function (b) Discontinuous Objective Function