Pinch analysis
Author: Micah Zuckerman [2015]
Stewards: Jian Gong and Fengqi You
Introduction
Pinch analysis is a methodology used to minimize energy consumption of chemical processes by optimizing energy recovery methods. A pinch occurs at the closest point of approach between hot and cold streams in the network. By designing around this point energy from utilities can be minimized. This page focuses on pinch analysis in the context of heat exchanger networks (HENs), however similar methods can be used in the design of mass exchanger networks (MENs).
Pinch technology
For maximum energy recovery (MER), energy should not be transferred across the pinch. The network is separated into hot and cold regions, above and below the pinch respectively. In the hot region, streams are matched so that heat is transferred from the coolest possible source. Below the pinch, the opposite occurs. This yields the minimum utility requirement solution to the heat exchanger network. Minimum utility requirement is not necessarily the optimum solution, however, the solution with the lowest overall cost is. Minimizing the size and quantity of heat exchangers plays a large role in decreasing capital costs. There is a trade-off between operational and capital costs. In some cases transfer across the pinch is necessary to produce the optimal network. For more information see the trade-off section of the Sensitivity analysis and design optimization page.
Minimum approach temperature
The minimum approach temperature represents the smallest gap in temperature across which heat transfer will occur in the system. This often only occurs at the pinch. While technically any value greater than zero can allow for heat transfer, very small values are not often feasible. Low temperature differences decrease the need for additional utilities, but require increasingly large heat transfer areas, meaning larger heat exchangers. The trade-off between operating costs and capital costs should be used to choose the minimum approach temperature for the network. Typical choices for minimum approach temperatures are between 5 °C and 30 °C (Towler 128).
Composite curves method
This method uses a graphical approach and makes obvious the presence and location of the pinch in the system. First one combines all hot streams into single composite curve on a temperature-enthalpy graph. The same is then done with the cold streams. Plotting both composite curves on a temperature-enthalpy plot reveals a pinch at the point where the cold and hot curves are closest in temperature. Because change in enthalpy is the feature of concern, the composite curves can be freely shifted along the enthalpy axis. In this manner the minimum approach temperature can be satisfied at the pinch.
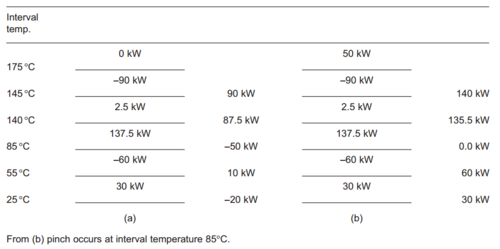
Problem table method
The problem table method, also known as the cascade method, forgoes graphs for a numerical approach. This method is useful when solving heat-exchanger network problems manually, but has fallen into disuse due to the advent of modern computing. The first step in the process is converting stream temperatures into interval temperatures. To do this, one sutracts half the minimum approach temperature from the hot stream temperatures, and adds half to the cold stream temperatures. The intervals are then ranked in order of magnitude, ignoring any repetitions. The next step involves balancing the heat carried by streams between each interval. Any excess heat cascades over into the next lower down interval. Add heat from the top of the system eliminate any negative values. The amount added at the top corresponds to hot utility duty, while the remaining value at the bottom corresponds to heat that must be removed by cold utility.
Computer tools for HEN design
Presently, pinch analysis is performed by specialized software the majority of the time in industry. Stream data is often pulled directly from the process simulations by the software package. Automatically generated networks must be properly constrained lest an unfeasible amount of stream splits and loops be generated. There is great value, however, in the ability of software packages to perform many tweaks and iterations to fine tune a network.
References
1. G.P. Towler, R. Sinnott, Chemical Engineering Design: Principles, Practice and Economics of Plant and Process Design, Elsevier, 2012.
2. L.T. Biegler, I.E. Grossmann, A.W. Westerberg, Systematic Methods of Chemical Process Design, Prentice-Hall: Upper Saddle River, 1997.
3. W.D. Sieder, J.D. Seader, D.R. Lewin, Process Design Principles: Synthesis, Analysis, and Evaluation, Wiley: New York, 2004.
4. R.T. Turton, R.C. Bailie, W.B. Whiting, J.A. Shaeiwitz, Analysis, Synthesis, and Design of Chemical Processes, Prentice Hall: Upper Saddle River, 2003.