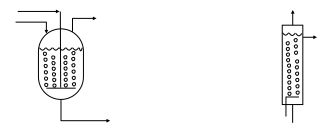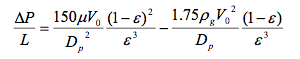Reactors: Difference between revisions
No edit summary |
Nataliamaj (talk | contribs) |
||
| (95 intermediate revisions by 5 users not shown) | |||
| Line 1: | Line 1: | ||
<br> |
|||
Title: Reactors |
Title: Reactors |
||
Authors: |
|||
Author: Sean Cabaniss, David Park, Maxim Slivinsky, and Julianne Wagoner [Winter 2014] |
|||
Sean Cabaniss, David Park, Maxim Slivinsky, and Julianne Wagoner <sup>[Winter 2014]</sup> |
|||
Neil Dalvie, KC Anderson, Natalia Majewska <sup>[Winter 2016]</sup> |
|||
Steward: David Chen, Fengqi You |
Steward: David Chen, Fengqi You |
||
| Line 15: | Line 17: | ||
The center of any chemical process is the reactor, where chemical reactions are carried out to transform feeds into products. Reactor design is a vital step in the overall design of a process. It is important to ensure that the equipment specified will be capable of achieving the desired yields and selectivity. |
The center of any chemical process is the reactor, where chemical reactions are carried out to transform feeds into products. Reactor design is a vital step in the overall design of a process. It is important to ensure that the equipment specified will be capable of achieving the desired yields and selectivity. |
||
=Second Introduction= |
|||
<p>This is another introduction about reactors. List of people who use reactors:</p> |
|||
Chemical Engineers |
|||
Chemical Engineering Students |
|||
Ralph |
|||
==Ideal Reactors== |
==Ideal Reactors== |
||
| Line 274: | Line 266: | ||
* Use physical modeling (“cold flow”) experiments |
* Use physical modeling (“cold flow”) experiments |
||
* Use tomography methods to look at performance of real reactor |
* Use tomography methods to look at performance of real reactor |
||
==Gas Mixing== |
==Gas Mixing== |
||
| Line 281: | Line 274: | ||
*'''Inline Mixing''' Inline mixers can be used for the continuous mixing of low-viscosity fluids. One inexpensive method involves the use of static devices that promote turbulent mixing in pipelines. Some typical designs are shown in Figures 2(a), (b), and (c). |
*'''Inline Mixing''' Inline mixers can be used for the continuous mixing of low-viscosity fluids. One inexpensive method involves the use of static devices that promote turbulent mixing in pipelines. Some typical designs are shown in Figures 2(a), (b), and (c). |
||
::[[File:Static_Mixers.PNG]] |
|||
::''Figure 2.'' Inline mixers: (a) tee; (b) injection; (c) annular (Towler and Sinnott, 2013) |
::''Figure 2.'' Inline mixers: (a) tee; (b) injection; (c) annular (Towler and Sinnott, 2013) |
||
| Line 471: | Line 463: | ||
Enzymes are the biological equivalent of catalysts. They can sometimes be isolated from host cells. They are usually proteins and, therefore, most are thermally unstable above ~60 degrees Celsius and active only in water at a restricted pH (Towler, 2012). Enzymes can sometimes be absorbed onto a solid or encapsulated in a gel without losing their structure. In this case, they can be used in a conventional fixed bed reactor. Typically, homogenous reactions are carried out in batch reactors. |
Enzymes are the biological equivalent of catalysts. They can sometimes be isolated from host cells. They are usually proteins and, therefore, most are thermally unstable above ~60 degrees Celsius and active only in water at a restricted pH (Towler, 2012). Enzymes can sometimes be absorbed onto a solid or encapsulated in a gel without losing their structure. In this case, they can be used in a conventional fixed bed reactor. Typically, homogenous reactions are carried out in batch reactors. |
||
===Microorganism Design and Selection=== |
|||
As an alternative to an enzyme catalyst, engineered microorganisms can be used to produce a chemical of interest. This product could be complex biological compounds, therapeutic proteins, or commodity plastics and fuels (Westfall 2011). Host cells as a platform for modification have so far included bacteria, yeast, and mammalian cells (Schmidt 2005). The efficiency of a bioreactor is heavily dependent on the efficiency of the microorganism used. An inefficient cell host that does a poor job of producing the desired product will always result in a poorly designed bioreactor, regardless of the equipment or conditions used. Furthermore, the design of a bioreactor is largely based around the ideal growth conditions of the microorganism. As shown in this section, the design and/or selection of a microbial host is closely related to the design of the bioreactor. Choice of a host demands particular reactor conditions, and in the case of genetically engineered microbes, the cells must be designed to operate in conditions that are feasible and affordable with modern bioreactor technology. This process can involve the rigorous engineering of a novel microorganism, a large screening for high producing strains, or, most likely, a combination of the two. This step of the bioreactor design process requires close collaboration between process engineering and microbiology. |
|||
====Fermentation Goals==== |
|||
Fermentation as a general practice is carried out with the following goals, many of which are effected directly by microorganism choice (Shuler 2002). |
|||
=====Cost, Yield, and Productivity===== |
|||
The goal of an efficient microbial host results in four parameters that relate microbe performance to the overall reactor performance. Overall fermentation performance for batch and fed batch processes can be evaluated as |
|||
::::::<math>\frac{dP}{dt}=q_{\text{p}}X</math> |
|||
where <math>P</math> represents the concentration of desired product, <math>X</math> the concentration of cells, and <math>q_{\text{p}}</math> the specific productivity in mass of product per mass of cells per time. Cell growth can be modeled by the equation |
|||
::::::<math>\frac{dX}{dt}=uX</math> |
|||
where <math>u</math> is the specific growth rate per time. Desirable values for these parameters for a scaled bacterial process are a productivity of 0.1 g/L-hr and a growth rate of 0.2-0.7 1/hr. As discusses later, these parameters are specific to cell lines, and are difficult to engineer orthogonally. |
|||
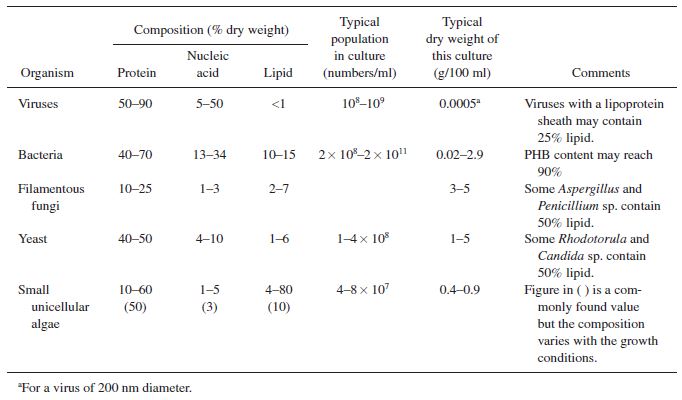
In addition to growth and product formation, it is important to consider substrate consumption in selecting an efficient microorganism. Often high product titers can be obtained with excessive waste of substrate, leading to extensive costs and unrealistic reactor sizes. In order to best understand substrate utilization, it is easiest to view the composition of the organism and the product as a whole to develop substrate requirements, shown in the following tables. |
|||
[[File:Cell_type_compositions.JPG|frame|center|Table 1. Rough compositions of common cell types.]] |
|||
[[File:Elementrequirements.JPG|frame|center|Table 2. Approximate elemental requirements.]] |
|||
While many elements are required, it is not necessary to model all of them. For evaluating the consumption of feed, it is useful to model the organism's chemical consumption on an elemental level for only the first four. |
|||
::::<math>C_{\text{w}}H_{\text{x}}O_{\text{y}}N_{\text{z}}+aO_{\text{2}}+bNH_{\text{3}}\rightarrow cCH_{\text{r}}O_{\text{s}}N_{\text{t}}+dCO_{\text{2}}+eH_{\text{2}}O+fC_{\text{j}}H_{\text{k}}O_{\text{l}}N_{\text{m}}</math> |
|||
where w,x,y,z indicate substrate composition, r,s,t indicate the relative cell composition, and j,k,l,m indicate the composition of the product. Alone, this design equation cannot be solved for a single solution. Instead, two additional parameters are required that are specific to the cell host. <math>Y_{\text{X/Sp}}</math> and <math>Y_{\text{P/S}}</math> represent the yield of cell mass and product mass per mass of fed substrate. These parameters characterize how the cell host utilizes its feed, and again are difficult to orthogonally engineer. Using this stoichiometric design equation and a desired product formation rate, the rate of substrate utilization can be calculated. In this way, the overall fermentation yield relies heavily on these four organism design parameters, <math>q_{\text{p}},u,Y_{\text{X/S}},</math> and <math>Y_{\text{P/S}}</math>. |
|||
For continuous fermentation, the process holds the same dependence on these parameters, which are found in the following design mass balance. |
|||
::::<math>FS_{\text{0}}-FS-\frac{VuX}{Y_{\text{X/S}}}-\frac{Vq_{\text{p}}X}{Y_{\text{P/S}}}=V\frac{dS}{dt}</math> |
|||
=====Product Isolation and Purification===== |
|||
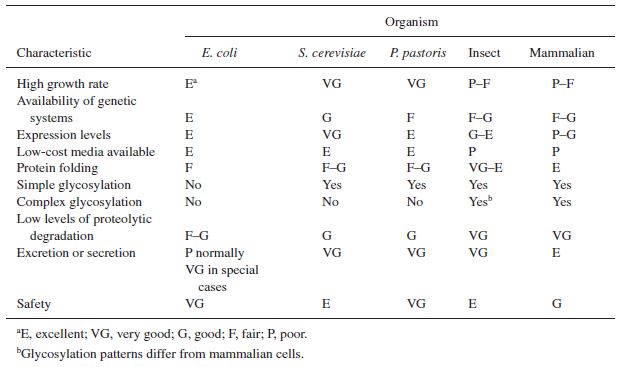
Downstream processing of the product is primarily dependent on the nature and chemical properties of the product itself. For example, a particular intracellular protein may be very difficult to separate from other cell internals. However, the choice of microorganism can have a significant impact on early separation steps, specifically the separation of the product from the cell mass. Paramount is whether or not the product is excreted from cells. Bacteria like ''E. coli'' lack many of the mechanisms required to excrete a desired product into the fermentation broth. This requires the lysing of cells in early downstream processing and separation of the product from cell internals. This process would be executed in batches, which can be timed optimally to maximize use of fermentation and separation equipment (Biegler 1997). On the other hand, mammalian cells and yeast can be engineered or screened to secrete the product of interest into the fermentation broth. This process removes the requirement of lysis step, and greatly simplifies the purification of product. This also makes the reactor particularly amenable to continuous fermentation (Huang 2008). Additionally, eukaryotic cells can produce more complex products, such as glycosylated protein. The glycosylation of proteins is a mechanism only recently achieved in bacteria (Nothaft, 2010).The table below indicates advantages and disadvantages of different types of organisms. |
|||
[[File:Cellcomparison.JPG|frame|center|Table 3. Cell type comparison.]] |
|||
=====Operation Conditions, Equipment, and Scale Up===== |
|||
It is important for the process engineer to select a microorganism that can operate within reasonable reactor conditions. |
|||
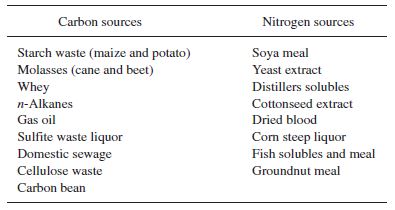
*Feed: The microbe must exhibit desirable design parameters when grown on a feed that is not commercially or cost restrictive. Below are several common bioreactor feeds. |
|||
[[File:Commonfeeds.JPG|frame|center|Table 4. Common affordable microbe feeds.]] |
|||
*Heat: The microbe must exhibit desirable design parameters at a temperature that is reasonable to maintain in a bioreactor. Because fermentation generates excessive heat from substrate breakdown, this generally involves cooling the reactor to between ambient and 37 C (Towler 2012). A microbial host that requires temperatures too high or low is not amenable to a controlled fermentation. This is especially salient with extremophiles - microbes that live in extreme conditions that often exhibit naturally high titers of high value products. In this case, it would be necessary to engineer the extremophile, or choose a more reasonable cell host. |
|||
*Oxygen: Microbes can generally grow in aerobic or anearobic conditions. Often, product formation and growth will be favorable in aerobic conditions. If this is the case, it is important to consider the oxygen requirement to maintain aerobic conditions, and ensure that the bioreactor designed can meet the requirements of the organism at the desired growth rates and concentrations. When designing a microorganism, it is important to not require an oxygen usage rate that is above what a reasonable bioreactor can provide. |
|||
====Challenges in Microorganism Design==== |
|||
Cells must be engineered to produce a heterologous product through recombinant DNA. For a therapeutic protein, this includes identifying the DNA sequence coding for the protein, and expressing that DNA in a cell host (Seider 2004). For a commodity molecule, enzymes that catalyze the synthesis of that molecule must be identified and expressed in the host cell. The engineering of microorganisms presents a number of formidable challenges. Many companies avoid this issue by screening known microorganisms for strains that naturally produce high titers of product, or close precursors. Expressing heterologous genes in cells causes high stress, and disrupts natural metabolic balance. |
|||
There are many techniques used for the engineering of microorganisms. These involved mostly the manipulation and delivery of heterologous DNA to the host cell line, to genetically manipulate its phenotype. However, because this wiki focuses on design for the process engineer, those techniques are left out of this discussion. Instead, the aspects of organism design that impact the process parameters exhibited by the organism will be elucidated. This mainly involves balancing the observed <math>Y_{\text{X/S}}</math> and <math>Y_{\text{P/S}}</math> to maintain high productivity and growth rate. |
|||
Metabolic engineering studies ways to relieve these stresses by “rewiring” synthesis networks within cells (Stephanopoulos 1998). This includes largely two parts. The first involves constructing non-native biochemical pathways in cells. This is necessary if the host does not already produce the desired product. Enzymes are expressed in the host that catalyze the correct reactions to synthesize the product. This often puts stress on cells, as it diverts resources in the cell towards the product that are typically utilized elsewhere, such as for growth. The second aspect of metabolic engineering involves the manipulation and balancing of metabolic fluxes within the cell. This involves controlling the expression of enzymes so that the cell makes enough product, but still has enough resources to grow to an acceptable level. Sometimes, it can be advantageous to only induce production of the product after cells have grown to a high concentration. This requires the heterologous DNA to be expressed with an inducible promoter. For example, production of a product could be induced when the feedstock is switched to methanol (Yurimoto 2000). |
|||
A parallel strategy to metabolic engineering is protein engineering. This simply involves the design or random testing of proteins, usually enzymes, to either enhance or alter their function. This is used in conjunction with metabolic engineering to either create novel pathways, or balance existing pathways. |
|||
====Case Studies==== |
|||
In this section, two case studies are considered. The production of penicillin stands as the first high profile selection of an industrial microorganism. The more modern production of artemisinin from bacteria serves as a canonical example of microorganism design. |
|||
=====Penicillin Production===== |
|||
In 1928, Alexander Fleming discovered that the mold ''Penicillium notatum'' produced a substance that would kill bacteria. The product was named penicillin, and was not studied for nearly 10 years. With the advent of World War II, the demand of effective antibiotics cause penicillin to be characterized. It was purified for study by biochemists, and found to be extremely effective. There now existed a demand for the mass production of the drug, which at that time had traditionally been done by chemical synthesis. However, the fragility and complexity of penicillin forced American pharmaceutical companies to pursue a fermentation process, taking advantage of the biological mechanisms already in place for the molecule's production. Designing this novel industrial process including two major challenges, both related to the selection of the optimal microorganism. First, the product was produced at low amounts, and increased product concentrations were necessary for industrial production. Second, the organism had to perform at a repeatable, characterizable, level on large scales with large, often anaerobic tanks. Hundreds of Penicillium strains were isolated and characterized, with ''Penicillium chrysogenum'' being selected, which produced penicillin at two orders of magnitude higher than other tested strains. This allowed a product concentration of 0.001 g/L in scaled bioreactors. This number is extremely low by today's standards, and presented a formidable purification challenge. Purification was assisted by the excretion of penicillin by the mold, a major advantage of eukaryotic fermentation. Today, after countless iterations of strain modification, product concentrations exceed 50 g/L (Shuler 2002). |
|||
=====Artemisinin Production===== |
|||
Artemisinin is an effective anti-malarial drug, and is the treatment of choice for the ''Plasmodium falciparum'' parasite. Up until a decade ago, access to this important drug was limited in several parts of the world. Since then, bioengineers have successfully designed microorganisms that can produce artemisinin at levels high enough to provide significant increases in worldwide accessibility. |
|||
Artemisinin is derived from the herb ''Artemisia annua''. Unfortunately, it is produced in trace levels in the plant. Purification is difficult and requires impossible amount of plant biomass. Efforts made to engineer the natural pathway of artemisinin synthesis have been met with little success. The synthesis pathway of artemisinin ''in vivo'' is largely unknown. While the genetic manipulation of the expression of several enzymes has increased yields, the production is not at a level amenable to a bioreactor. In parallel, strategies to produce artemisinin through chemical synthesis or biochemical pathways ''in vitro'' have met similar challenges. |
|||
Success in artemisinin production has come in the form of engineered microorganisms. The highest production titers to date are the result of the heterologous expression of enzyme pathways from plants in both the bacteria ''Escherichia coli'' and the yeast ''Saccharomyces cerevisiae'', with ''E. coli'' seeing more success. Currently, ''E. coli'' can achieve 450 mg/L of product after 60 hours, and ''S. cerevisiae'' can achieve 153 mg/L over 16 days. These successes were met using three techniques. First, metabolic pathways for artemisinin precursors were assembled in the microorganisms from a number of sources. Second, several enzymes were mutated to improve or slightly alter their function. Third, gene expression of each enzyme was tuned to optimize the amount of enzyme needed for each synthetic step. These techniques allowed the productivity of the cells to remain high while retaining a stable growth rate. Microorganisms that exhibit this balance of cell yield and product yield are ideal for bioreactors (Arsenault 2010). |
|||
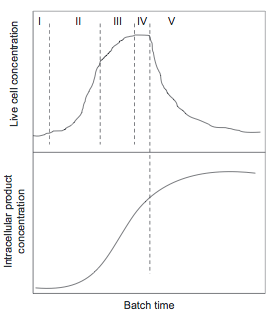
===Cell Growth=== |
===Cell Growth=== |
||
| Line 485: | Line 557: | ||
* IV: Stationary phase: cell growth rate and death rate are equal |
* IV: Stationary phase: cell growth rate and death rate are equal |
||
* V: Decline phase: cells die or sporulate, often caused by product build-up |
* V: Decline phase: cells die or sporulate, often caused by product build-up |
||
'''Innoculation''' |
|||
The Innoculation, or Lag phase is the first step of cell growth during a batch fermentation process. There is a minimal increase in cell density. This phase is least understood by scientists but has been noticed since the end of the 19th century. There is a lack of data that can adequately explain the physiological and molecular processes that take place during this phase. |
|||
'''Exponential Growth''' |
|||
The exponential phase, also known as the logarithmic growth phase, occurs when cells adjust to their new conditions. They are diving at a constant rate resulting in an exponential increase in cells following first order kinetics. The equation below illustrates this process: |
|||
<div style="text-align: center;"><math>\frac{dX}{dt}= X\left(\mu-K_{d} \right)</math></div> |
|||
Cell growth is often substrate limited, meaning the growth will plateau once substrates become less available. Cell growth rate can be measured by different forms of inhibition. These forms include substrate inhibition, product inhibition, and toxic compounds inhibition. |
|||
'''Stationary Phase''' |
|||
Stationary phase occurs when the number of cells dying and dividing reaches an equilibrium. This can be caused due to the depletion of one or more growth nutrients, the accumulation of toxic byproducts, the induction of a gene. Induction causes a stressful environment for cells and increases the death rate. In this phase, production of the primary metabolite stops, but the production of a secondary metabolite can continue. |
|||
'''Decline Phase''' |
|||
The decline, or death phase occurs when the rate of cell death is greater than of cell generation. It is represented by the following first order kinetics equation: |
|||
<div style="text-align: center;"><math>\frac{dX}{dt}= -K_{d}X</math></div> |
|||
'''Measuring Growth''' |
|||
One easy way to quickly establish a growth curve is to measure the optical density with a spectrophotometer. A sample of the fermentation liquid is taken up and the absorbance of the sample is measured with the spectrophotometer. The measured value is then combined with previous measurements and a curve can be constructed. One drawback of this method is that both viable and non-viable cells are measured and taken into account. |
|||
Intracellular product accumulation is slow at first because there are a limited number of cells (Towler, 2012). However, it is important to note that product accumulation continue even after the live cell count falls, since dead cells still contain product. |
Intracellular product accumulation is slow at first because there are a limited number of cells (Towler, 2012). However, it is important to note that product accumulation continue even after the live cell count falls, since dead cells still contain product. |
||
| Line 499: | Line 598: | ||
All of these factors are exacerbated at higher cell concentrations (Towler, 2012). Clearly, biological reactions must be carefully controlled. An addition complication in dealing with biological reactions is that the product formation is often not closedly tied to the rate of consumption of the substrate (Towler, 2012). This is because of the fact that the product may be made by the cells at a relatively low concentration and the fact that some cell metabolic processes may not be involved in formation of the desired product (Towler, 2012). |
All of these factors are exacerbated at higher cell concentrations (Towler, 2012). Clearly, biological reactions must be carefully controlled. An addition complication in dealing with biological reactions is that the product formation is often not closedly tied to the rate of consumption of the substrate (Towler, 2012). This is because of the fact that the product may be made by the cells at a relatively low concentration and the fact that some cell metabolic processes may not be involved in formation of the desired product (Towler, 2012). |
||
===Batch or Continuous=== |
|||
'''Batch''' |
|||
Batch bioreactors represent the majority of industrial processes. This requires a sterilization phase and inoculation of the culture medium with microorganisms before the reaction can occur. Some advantages of batch systems include (William, 2002): |
|||
* A reduced risk of contamination due to a short growth time |
|||
* Lower capital investment |
|||
* More flexibility for biological systems |
|||
Some disadvantages include: |
|||
* Intermediate steps that cause decreased productivity levels |
|||
* High expense when preparing culture for inoculation |
|||
* Higher hygiene risks due to close contact with microorganisms |
|||
'''Continuous''' |
|||
For a continuous process, media that is either sterile or contains bacteria is continuously fed into a bioreactor in order to hold the steady state. Some advantages of continuous systems include (William, 2002): |
|||
* Potential for automation |
|||
* Lower costs of labor |
|||
* Less time spent sterilizing and preparing |
|||
* Consistent product quality |
|||
Some disadvantages include: |
|||
* Only small changes in process are allowed |
|||
* Feed quality needs to be specified and maintained |
|||
* Higher investment costs |
|||
* Risk of cell mutation due to short cultivation |
|||
'''Case Study: Batch vs Continuous''' |
|||
A research group compared the rates of production of the enzyme xylanase. Filamentous fungi secrete this enzyme into the medium during fermentation and have much higher activity than yeast and bacteria. This enzyme increases the body weight gains of animals. It is also used in prebleaching in the paper industry as well as helps regulate dough viscosity in the baking industry. Finally, it can be used for the production of fuel and chemical feedstocks (Bakri, 2012). |
|||
Due to the nature of continuous condition, the group predicted that this option should yield higher results. Continuous fermentation does not require time to clean up and sterilize new batches. The cells were grown in a 3 liter Electro-lab fermenter with a barley straw hydrolase medium. For the batch portion of the experiment, the reactor was filled with 1.5 liters of medium and was inoculated with a concentration of a million spores per milliliter. For the continous portion of the experiment, the medium was pumped into the bioreactor using a peristaltic pump at a speed of 75 milliliters per hour. The speed was chosen to allow for the retention of 1.5 liters of culture during the process (Bakri, 2012). |
|||
The results for both batch and continuous methods are illustrated below: |
|||
[[file:batch.png | 300x400px]] |
|||
''Figure 16: Xylanase production using batch method'' |
|||
[[file:cont.png | 300x400px]] |
|||
''Figure 17: Xylanase production using continuous method'' |
|||
[[file:batch_v_cont.png | 300x400px]] |
|||
''Figure 18: Xylanase productivity comparing batch and continuous method'' |
|||
This case study shows that although the concentration of xylanase was higher in batch mode, the highest productivity occurred in the continuous method. The productivity increased by almost eight fold, showing that a continuous culture is the best production method (Bakri, 2012). |
|||
===Mass Transfer for Bioreactors=== |
|||
Mass transfer is important to keep in mind because it often becomes the limiting step of the overall process. The volumetric oxygen transfer coefficient must be known to accurately design and scale up bioreactors. The following equation shows the mass balance for dissolved oxygen in a well-mixed reactor with the absence of biomass: |
|||
<div style="text-align: center;"><math>\frac{dC}{dt}= K_{\text{La}}\left(C*-C \right)</math></div> |
|||
The variables that affect the <math>K_{\text{La}}</math> values are mostly affected by impeller configuration, speed and aeration. An increase in the gas flow rate makes the <math>K_{\text{La}}</math> values increase (Karimi, 2013). |
|||
===Types of Bioreactors=== |
===Types of Bioreactors=== |
||
| Line 517: | Line 675: | ||
::''Figure 15.'' Examples of shaftless bioreactors (Towler, 2012) |
::''Figure 15.'' Examples of shaftless bioreactors (Towler, 2012) |
||
* '''WAVE Bioreactors''' |
|||
:: WAVE bioreactors represent an alternative to standard stainless steel bioreactors. These reactors are flexible and single-use, cutting down time between batches and allow for a more sterile environment. These disposable reactors are mostly used in mammalian cell culture. Three layers of plastic are the minimum necessary for construction. The first is a structural layer, followed by a barrier layer that allows for permeability. The last layer, the fluid contact layer, is designed to take into account inertness and maintain a good seal (Bioprocess, 2013). |
|||
::[[File:Wave.jpg]] |
|||
::''Figure 16.'' Example of a WAVE bioreactor (GE Health, 2016). |
|||
* '''Packed Bed Bioreactors''' |
|||
:: Packed Bed Bioreactors are structured so that the cells are immobilized and placed on large particles. Although they are relatively simple to construct, they can have blockage issues or poor oxygen transfer. There are three types of flow: downward flow, upward flow and the recycling method. In industry, upward flow is preferred, especially when there is gas production during the fermentation (Prieto, 2003). |
|||
::[[File:Packed1.png]] |
|||
::''Figure 17.'' Example of a packed bed bioreactor (Kang, 2000). |
|||
* '''Anaerobic Bioreactors''' |
|||
:: Anaerobic reactions are used in ethanol production, winemaking, beer brewing, and wastewater treatment. Due to its long standing history, these processes have become well established and improvements include decreasing cost of production due to new technology. Although continuous production for beer has been patented on a large scale, most investment is still focused on batch production (William, 2002). |
|||
===Preventing Contamination=== |
|||
Since cells are easily affected by both unwanted chemicals and other species in the reactor, bioreactors must be designed in order to avoid contamination (Towler 2013). Bacterial spores are the most demanding sterilization challenge in a bioreactor. Bacterial spores are dormant and non-reproductive structures produced by a small number of bacteria. Since they are meant to ensure survival of bacteria in times of environmental stress, they are heat resistant. In order to ensure that all spores within the medium are killed, the medium must be sterilized (Shuler 2002). There are many methods of sterilization, including filtering, chemical, thermal, and radiation. Thermal sterilization using steam is the most common method, as it is the most economical method for large scale reactors. Chemical agents cannot be toxic to the product, and UV radiation cannot penetrate fluids easily. Steam sterilizations either occur in the fermentation vessel as a batch sterilization or in a continuous apparatus upstream of the fermentation vessel (Seider 2004). |
|||
====Death Kinetics==== |
|||
:: The death kinetics involved in sterilization can usually be described by first order kinetics, but since essentially all contaminants need to be removed, it is usually described in probabilistic terms (Towler 2013). The specific death rate of an organism for thermal inactivation can be described as |
|||
::<math>k_d = \alpha e^{-E_{\text{0d}} / RT}</math> |
|||
:: where <math>k_d</math> is the specific death rate, <math> \alpha </math> is the Pre-Arrhenius constant, <math>E_{\text{0d}}</math> is the activation energy for individual death, and T is the temperature. Sterilization is usually designed for Bacillus stearothermophilus since it is one of the most heat resistant potential contaminants. The death rate for the vitamins in the media must also be considered when designing sterilization, since the nutritional value of the media can be damaged. Short time, high temperature treatment to sterilize media can ensure that the nutritional value is not damaged, but the spores are killed. Typical values for the pre-Arrhenius constant are 1*10^36 and 1*10^4 min^-1 for spores and vitamins respectively. Typical values for the activation energy for individual death are 65 and 10kcal/mol for spores and vitamins respectively (Jewett 2016). |
|||
::The number of viable individuals after sterilization can then be described as |
|||
::<math> N / N_0 = e^{-k_dt}</math> |
|||
:: where N is the number of viable individuals, <math>N_0</math> is the number of contaminants initially present, and t is time. The probability of having a contaminated culture can then be described as |
|||
::<math>1-P_0(t) = 1 - (1 - e^{-k_dt})^{N_0}</math> |
|||
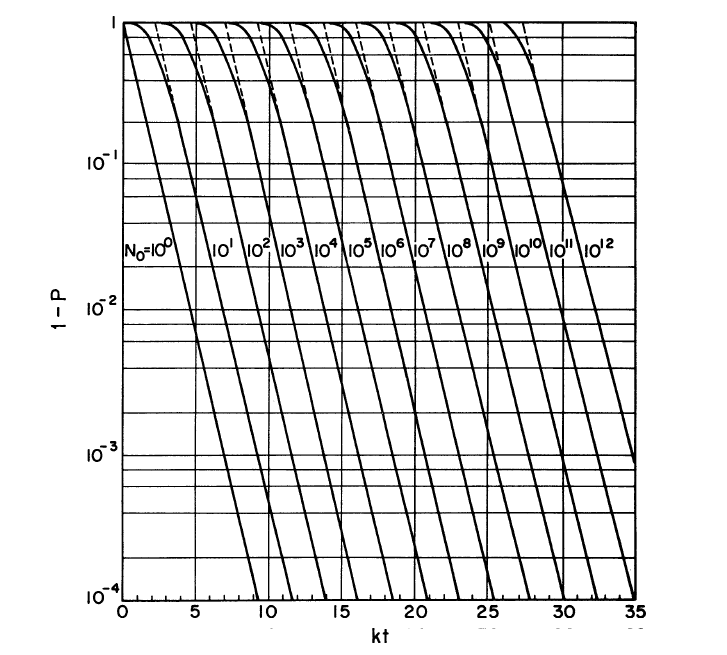
:: This probability can also be determined with a sterilization chart, using the spore challenge (<math>N_0</math>) and <math>k_dt</math>, as shown in Fig. 16. The same equations are used for both batch and continuous sterilization, but the spore challenge will be calculated differently, which will be discussed in further sections (Shuler 2002). |
|||
::[[File:Sterilizationchart.PNG]] |
|||
::''Fig. 18.'' Sterilization chart (Shuler 2002). |
|||
====Sterilization of Liquids==== |
|||
=====Batch===== |
|||
::Batch sterilization is used for smaller fermenters (Biegler 1997). It is usually performed at 121˚C. This is the more widely used technique, since it is a simpler operation than continuous sterilization and no additional materials are added to the media. The disadvantages of batch sterilization are thermal lags and incomplete mixing. Heating requirements are also greater. (DiLeo 2000). The heat up and cool down times from 121˚C to 37˚C are usually longer than the time at the sterilization temperature and can damage the vitamins and protein in the media (Shuelr 2002). The spore challenge for batch sterilization can be calculated with the following equation |
|||
::<math>N_0 = n_0V_\text{total} </math> |
|||
::where <math>n_0</math> is the concentration of spores in the media initially and <math>V_\text{total}</math> is the total volume of media (Shuler 2002). |
|||
=====Continuous===== |
|||
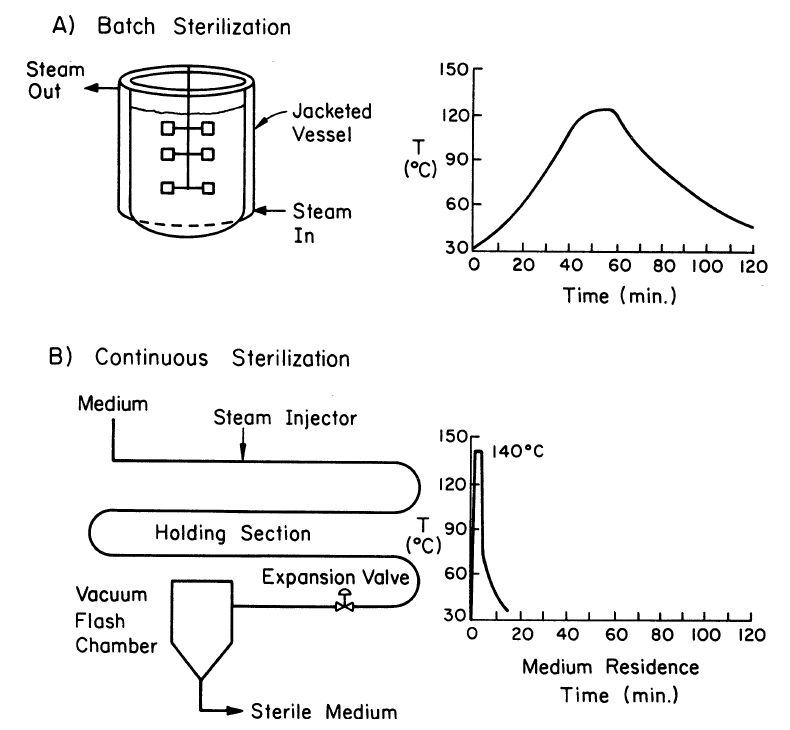
:: The short-exposure and high temperature of continuous sterilization is easier to control, does less damage to the medium, and reduces fermenter downtime. It is also more efficient since it heats small portions of the inlet stream at a time rather than using energy to heat, hold, and cool the entire volume of media at the same time. (DiLeo 2000). The disadvantages, however, are dilution of the medium with steam injection and foaming. (Shuler 2002). A common process for continuous sterilization consists of steam injected into the medium in order to heat it, passing the medium through a holding section to achieve the desired residence time, and then flash cooling the medium. Flash cooling prevents contamination from cooling water (Towler 2013). Diagrams and temperature profiles of batch and continuous sterilization is shown in Fig. 19. The spore challenge for continuous sterilization can be calculated with the following equation |
|||
::<math> N_0 = n_0(V_\text{loop}/ \tau)(t)</math> |
|||
:: where <math>V_\text{loop}</math> is the hold up volume in the reactor, <math>\tau</math> is the residence time, and t is the time spent in continuous mode (Jewett 2016). |
|||
::[[File:Sterilization.PNG]] |
|||
:: ''Fig. 19.'' Diagrams and temperature profiles of batch and continuous sterilization (Shuler 2002). |
|||
::Problems involved in sterilization increase greatly with scale-up, as sterilization methods used for lab-bench scale reactions are not acceptable for industry-scale reactions. Given the same medium, a sterilization temperature and time may be enough for a small scale reactor but not for a larger scale. For example, given a <math>k_dt</math> of 15 and <math>n_0</math> of 10^4 spores/L, the probability of contamination in a 1L reactor will be 0.003, and in a 10,000 L reactor will be about 1. |
|||
:: '''Other considerations''' |
|||
:: Since spores will germinate in a moist environment, making them easier to kill as vegetative cells, moist heat is preferred for sterilization. Connections in sterilization equipment must be steam sterilized and trapped air pockets should be avoided. Pipes should be sloped in order to avoid condensate pools and equipment should be pressure tested for leaks. It should be ensured that no viable host cells are in the waste streams and escape to the environment, and exit gas streams also need to be filtered to prevent the escape of microbes to the environment (Jewett 2016). |
|||
:: If the medium being sterilized contains heat-sensitive materials, filter sterilization must be used instead of steam. Filtration is also used to sterilize the process air used in the system. Microporous filters are used, so the medium must be prefiltered for larger particulates so that the microporous filter does not get clogged. However, filtration is not as reliable as steam sterilization, as any defects in the membrane can lead to contamination, and viruses can often pass through the filter (Shuler 2002). |
|||
=====Example Calculations===== |
|||
A continuous culture is ran in a 1,000L fermentor, and it is desired to have only one in one thousand chance of spore contamination. The fermentation is ran for four weeks at a dilution rate of 0.1hr^-1. The medium initially contains 10^5 spores/L. A sterilization temperature of 140C is used. <math>\alpha</math> for the spores is 1*10^36 min^-1, and <math>E_\text{0d}</math> is 67kcal/mol. There is a key temperature-sensitive vitamin in the broth at a concentration of 10mg/L that has <math>\alpha</math> of 1*10^4 min^-1 and <math>E_\text{0d}</math> of 10 kcal/mol (Jewett 2016). |
|||
* To calculate the time needed to sterilize the medium: |
|||
::<math>V_\text{total} = 1000L + (1000L*0.1hr^\text{-1} * 24hr/day * 7days/week * 4 weeks) = 68,200L</math> |
|||
::<math>N_0 = 68,200L * 10^5 spores/L = 6.82*10^9 spores</math> |
|||
::Use the sterilization chart (Fig. 18), with <math>1-P_0 = 10^-3</math> and <math>N_0 = 6.82*10^9</math>, to get <math>k_d^\text{spores}t = 29</math> |
|||
::To find k_d, |
|||
::<math>k_d^\text{spores} = \alpha e^{-E_\text{0D}/RT}</math> |
|||
::<math>k_d^\text{spores}= 10^{36}min^{-1}e^{-67,0000\text{cal/mol} / 1.987\text{cal/molK}*413K} = 3.59 min^{-1}</math> |
|||
::Using |
|||
::<math>k_d</math> and <math>k_dt</math> |
|||
::find <math>t</math> |
|||
::<math>k_d^\text{spores}t = 29 = 3.59*t</math> |
|||
::<math>t = 8.08min</math> |
|||
* To find the concentration of active vitamin after sterilization, |
|||
::First find |
|||
::<math>k_dt</math>, |
|||
::<math>k_d^\text{vitamin} = \alpha e^{-E_\text{0D}/RT}</math> |
|||
::<math>k_d^\text{vitamin}= 10^{4}min^{-1}e^{-10,0000\text{cal/mol} / 1.987\text{cal/molK}*413K} = 0.051 min^{-1}</math> |
|||
::Then use the equation, |
|||
::<math>N/N_0 = e^{-k_d^{vitamin}t}</math> |
|||
::<math>N/10\text{mg/L} = e^{-0.051min^{-1}*8.08min}</math> |
|||
::<math>N= 6.6 mg/L vitamin</math> |
|||
====Sterilization of Gases==== |
|||
:: Almost all biopharmaceutical production processes involve aeration and therefore require huge volumes of air. For a fermentation lasting five days, up to 200,000,000L of air could be required, and since it is being pumped into the medium, the air must be completely sterile. Air typically has a concentration of microbes of about 1-10 microbes per liter. |
|||
:: Compressors are required for such large volumes of air, and the adiabatic compression of the air increases the temperature to about 150-220C, and in order to kill spores, the air needs to be at about 220C for about thirty seconds. Therefore, the compression helps to sterilize the air, but since the air cools rapidly as it exits the compressor, and the pipes are hard to maintain as sterile, filtration is necessary to ensure that the entering air is still sterile after it exits the compressor and enters the reactor. |
|||
:: Filtration of gases is done by either depth or surface filters. In the past, carbon beds with glass wool was used as a depth filter, but if the filter became wet, it would no longer function, as the wet filter provided an easy path for contaminant penetration. The contaminant also needed to come into contact with the glass wool and stick to be stopped. These filters are damaged by steam sterilization, as they show hardening and shrinkage over time. Membrane cartridge filters as surface filters are now more commonly used in industry, as they can get wet and continue to stop contaminants. These filters utilize a sieving effect to remove particles, as membranes have a uniformly small pores that prevent the passage of particles with a larger radius. These filters can also be steam-sterilized without being damaged. Both types of filters increase the pressure drop in the reactor, since the price of energy needed for compressed air for these processes is large, and air treatment can account for a quarter of production costs. However, since high costs are associated with the loss of a batch to contamination, one has to balance the sterility provided from a given filter with minimizing the pressure drop in the reactor (Shuler 2002). |
|||
====Sterile Sampling==== |
|||
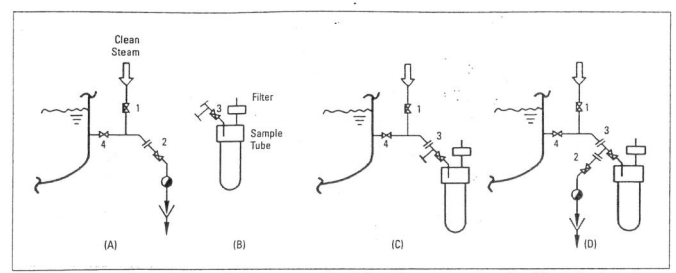
:: Sampling the medium in the reactor is necessary to ensure product quality, but it also carries the risk of introducing contamination into the medium. Sampling is usually done about five time a day for a bioreactor. A typical sampling device is shown in Fig. 20. The sampling valve on the reactor is connected to a steam trap to maintain a steam barrier between the reactor and the environment. A sterilized sampling device is attached to the reactor and a valve is attached to the sampling device. Steam runs through the system for about thirty minutes, and then the valves on the reactor and the sampling device are opened to remove the sample (Chisti 1992). |
|||
::[[File:Sampling.PNG]] |
|||
:: ''Figure 20.'' Diagram of typical sampling device with filter (Chisti 1992). |
|||
====Cleaning==== |
|||
::Cleaning the fermentation vessel at the end of the production run is necessary in order to remove residual substrates that could lead to contamination of future batches. Cleaning consists of the following wash steps: |
|||
::1. Wash with high-pressure water jets |
|||
::2. Wash with an alkaline cleaning solution, usually 1M NaOH |
|||
::3. Rinse with tap water |
|||
::4. Wash with an acidic cleaning solution, usually 1M nitric or phosphoric acid |
|||
::5. Rinse with tap water |
|||
::6. Rinse with deionized water |
|||
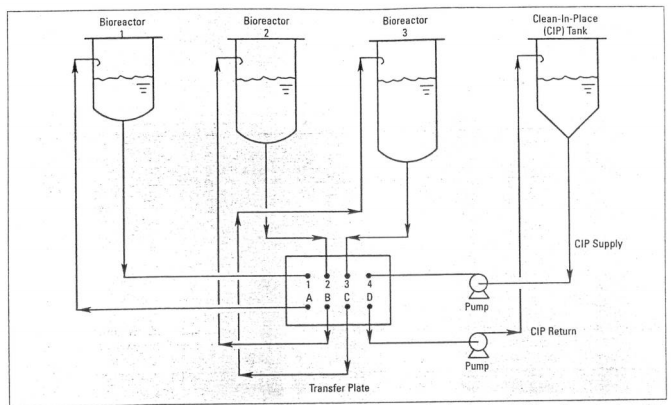
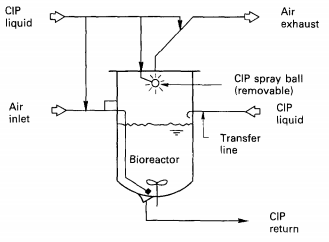
::The vessel is drained after each of these steps. For this reason, the vessel should have no internal dead spots where material could accumulate. Also, due to the repeated emptying and filling of the vessel, cleaning leads to significant down time between batches (Towler 2013). A clean-in-place (CIP) system with a transfer flow plate can make cleaning easier, as it connects all the bioreactors and transfer pipes in a plant to one cleaning system, as seen in Figure 21 and 22. The transfer plate has removable pipe sections, providing assurance against mixing of different bioreactor contents (Chisti 1994). |
|||
::[[File:cleaning.PNG]] |
|||
:: ''Figure 21.'' Example of a clean-in-place system with three bioreactors and a CIP tank (Chisti 1992). |
|||
::[[File:cleaning2.PNG]] |
|||
:: ''Figure 22.'' Delivery of CIP liquids to a bioreactor (Chisti 1994). |
|||
=Heating and Cooling of Reacting Systems= |
=Heating and Cooling of Reacting Systems= |
||
| Line 618: | Line 919: | ||
Turton R, Bailie RC, Whiting WB, Shaewitz JA, Bhattacharyya D. Analysis, Synthesis, and Design of Chemical Processes. 4th ed. Upper Saddle River: Prentice-Hall; 2012. |
Turton R, Bailie RC, Whiting WB, Shaewitz JA, Bhattacharyya D. Analysis, Synthesis, and Design of Chemical Processes. 4th ed. Upper Saddle River: Prentice-Hall; 2012. |
||
Westfall, Patrick J., and Timothy S. Gardner. "Industrial fermentation of renewable diesel fuels." Current opinion in biotechnology 22.3 (2011): 344-350. |
|||
Schmidt, F. R. "Optimization and scale up of industrial fermentation processes." Applied microbiology and biotechnology 68.4 (2005): 425-435. |
|||
Yurimoto, Hiroya, et al. "Regulation and evaluation of five methanol-inducible promoters in the methylotrophic yeast Candida boidinii." Biochimica et Biophysica Acta (BBA)-Gene Structure and Expression 1493.1 (2000): 56-63. |
|||
Huang, Hua-Jiang, et al. "A review of separation technologies in current and future biorefineries." Separation and Purification Technology 62.1 (2008): 1-21. |
|||
Stephanopoulos, George, Aristos A. Aristidou, and Jens Nielsen. Metabolic engineering: principles and methodologies. Academic press, 1998. |
|||
Nothaft, Harald, and Christine M. Szymanski. "Protein glycosylation in bacteria: sweeter than ever." Nature Reviews Microbiology 8.11 (2010): 765-778. |
|||
Shuler, ML, Kargi, F. Bioprocess Engineering Basic Concepts. 2nd ed. Upper Saddle River: Prentice-Hall. 2002: 315-320 |
|||
L.T. Biegler, I.E. Grossmann, A.W. Westerberg, Systematic Methods of Chemical ProcessDesign, Prentice-Hall: Upper Saddle River, 1997. |
|||
Shuler, Michael L., and Fikret Kargi. Bioprocess engineering. New York: Prentice Hall, 2002. |
|||
Arsenault, Patrick R., Kristin K. Wobbe, and Pamela J. Weathers. "Recent advances in artemisinin production through heterologous expression." Current medicinal chemistry 15.27 (2008): 2886. |
|||
Karimi, Ali, Golbabei, Farideh, Pourmand, Mohammad. “Oxygen mass transfer in a stirred tank bioreactor using different impeller configurations for environmental purposes.” Iranian Journal of Environmental Health, Science, and Engineering, 2013. |
|||
“WAVE Bioreactor 500/1000 System.” Bioprocess Online, 2013. |
|||
“WAVE Bioreactors.” GE Healthcare Life Sciences, 2016. |
|||
Prieto, G., Okumoto, M., Gay, C.R. “Nonthermal plasma reactors for the production of light hydrocarbon olefins from heavy oil.” Brazilian Journal of Chemical Engineeirng, 2003. |
|||
Kang, Xuezhen. “Packed Bed Bioreactor.” 2000. |
|||
Y. Chisti, Assure Bioreactor Sterility, Chemical Engineering Process. 1992: 88(9): 80-85. |
|||
M. Jewett. Media Design. ChBE 375: Biochemical Engineering Class Notes. January 12, 2016. |
|||
Y. Chisti, M. Moo-Young. Clean-in-place systems for industrial bioreactors: design, validation and operation. Journal of Industrial Microbiology. 1994: 13: 201-207. |
|||
G. DiLeo and S. Ogoreuc. “Sterilization”. Rensselaer Polytechnic Institute. 2000. http://www.rpi.edu/dept/chem-eng/Biotech-Environ/Projects00/sterilize/sterilization.html. Accessed February 20, 2016. |
|||
Y. Bakri, Y. Akeed, P. Thonart. "Comparison between continuous and batch processing to produce xylanase by penicillium canescens 10-10c." Brazilian Journal of Chemical Engineering, 2012. |
|||
Latest revision as of 00:56, 22 February 2016
Title: Reactors
Authors:
Sean Cabaniss, David Park, Maxim Slivinsky, and Julianne Wagoner [Winter 2014]
Neil Dalvie, KC Anderson, Natalia Majewska [Winter 2016]
Steward: David Chen, Fengqi You
Date Presented: February 4, 2014
Introduction
The center of any chemical process is the reactor, where chemical reactions are carried out to transform feeds into products. Reactor design is a vital step in the overall design of a process. It is important to ensure that the equipment specified will be capable of achieving the desired yields and selectivity.
Ideal Reactors
Batch Reactors
In a batch reactor, the reagents are added together and allowed to react for a given amount of time. The compositions change with time, but there is no flow through the process. Additional reagents may be added as the reaction proceeds, and changes in temperature may also be made. Products are removed from the reactor after the reaction has proceeded to completion.
Batch processes are suitable for small-scale production (less than 1,000,000 lb/yr) and for processes where several different products or grades are to be produced in the same equipment (Douglas, 1988). When production volumes are relatively small and/or the chemistry is relatively complex, batch processing provides an important means of quality control.
Plug Flow Reactor (PFR)
A PFR with tubular geometry has perfect radial mixing but no axial mixing. All materials hav the same residence time, τ, and experience the same temperature and concentration profiles along the reactor. Equation for PFR is given by:
where M = molar flow rate, dV is the incremental volume, and is the rate of reaction per unit volume.
This equation can be integrated along the length of the reactor to yield relationships between reactor resident time and concentration or conversion.
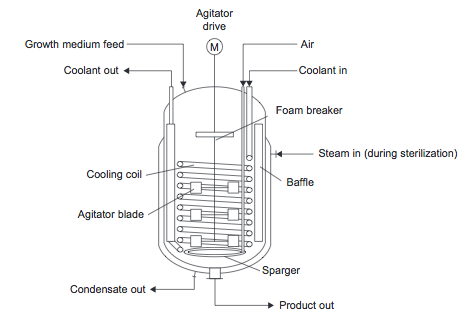
Continuously Stirred Tank Reactor (CSTR)
The stirred tank reactor models a large scale conventional laboratory flask and can be considered to be the basic chemical reactor. In a CSTR, shown in Figure 1, there is no spatial variation- the entire vessel contents are at the same temperature, pressure, and concentration. Therefore the fluid leaving the reactor is at the same temperature and concentration as the fluid inside the reactor.
The material balance across the CSTR is given by:
Some of the material the enters the reactor can leave immediately, while some leaves much later, so there is a broad distribution in residence time as shown in Figure 1.
Figure 1. Continuously Stirred Tank Reactor (Towler and Sinnott, 2013)
More information on stirred tanks can be found in the Mixing section.
General Reactor Design
The design of the reactor should not be carried out separately from the overall process design due to the significant impact on capital and operating costs on other parts of the process (Towler and Sinnott, 2013).
Step 1: Collect Required Data
Out of all process equipment, reactor design requires the most process input data: reaction enthalpies, phase-equilibrium constants, heat and mass transfer coefficients, as well as reaction rate constants. All of the aforementioned parameters can be estimated using simulation models or literature correlations except for reaction rate constant constants, which need to be determined experimentally (Towler and Sinnott, 2013).
Enthalpy of Reaction
- The heat given out in a chemical reaction is based on the enthalpies of the component chemical reactions, which are given for standard temperature and pressure (1 atm, 25 C). Values for standard heats of reaction can be found tabulated in literature, or can be calculated from heats of formation or combustion. Care must be taken to quote the basis for the heat of reaction and the states of reactants and products.
- The following equation is used to convert enthalpies from standard conditions to the process conditions:
- If the effect from pressure is not significant and only Temperature needs to be accounted for, the following equation should be used:
Equilibrium Constant and Gibbs Free Energy
- Where is the change in Gibbs free energy from the reaction at temperature , is the ideal gas constant, and is the reaction equilibrium constant, given by:
- where is the activity of component i, is the stoichiometric coefficient of component , and is the total number of components.
- Equilibrium constants can be found in the literature and are useful for evaluating the rates of forward and reverse reactions. Care must be taken to the experimental design used for the literature equilibrium constants to make sure they are consistent with the conditions of the actual process reactor. For more complicated reactions consisting of several sequential or simultaneous reactions, the equilibrium is found by minimizing the Gibbs free energy (Towler and Sinnott, 2013). Commercial process simulation programs use the Gibbs reactor model in this way.
Reaction Mechanisms, Rate Equations, and Rate Constants
- In most cases the main process reaction rate equations and rate constants cannot be predicted from first principles and must be approximated (Towler and Sinnott, 2013). This is due to the following:
- Use of heterogeneous catalysis or enzymes which lead to Langmuir-Hinshelwood-Hougen-Watson or Michaelis-Menten kinetics
- Mass transfer between vapor and liquid or two liquid phases
- Multistep mechanisms whose rate expressions do not follow overall reaction stoichiometry
- Competing side reactions
- As a result the main process reaction is usually approximated as first- or second-order over a narrow range of process conditions (temperature, pressure, species concentrations) to estimate the residence time required for a target conversion. Rate equations are always a fit for experimental data and should thus be used for interpolation within the data. It is important to collect more data when extrapolating, especially for exothermic reactions which have the potential for runaway (Towler and Sinnott, 2013).
Heat and Mass Transfer Properties
Heat Transfer
- The design of internal heating or cooling devices can be found in Heat Transfer Equipment. Correlations for tube-side heat-transfer coefficients for catalyst-packed tubes of a heat exchanger are given below:
- For heating:
- and for cooling:
- where is the tube-side heat transfer coefficient for a packed tube, is the tube diameter, is the fluid thermal conductivity, is the fluid density, is the superficial velocity, is the effective particle diameter, and is the fluid viscosity.
Diffusion Coefficients
- Diffusion coefficients are necessary when mass transfer can limit the rate of reaction, such as in catalytic reactions or reactions involving mass transfer processes such as gas absorption, distillation, and liquid-liquid extraction.
- The diffusivity for gases can be estimated by the following correlation (Fuller, Schettler, Giddings):
- where is the diffusivity, is temperature, are the molecular masses of components and , is the total pressure, and are the summation of special diffusion volume coefficients for components and , given in the table below:
- (volume coefficient table from towler)
- Wilke and Chang developed a correlation for estimating the diffusivity of components in the liquid phase:
- where is the liquid diffusivity, is an association factor for the solvent, is the molecular mass of the solvent, is the solvent viscosity, is the temperature, and is the molar volume of the solute at its boiling point. This correlation holds for organic compounds in water but not for water in organic solvents.
Mass Transfer
- For multiphase reactors it is necessary to estimate the mass transfer coefficient.
- The equation of Gupta and Thodos predicts the mass transfer coefficient for a packed bed of particles:
- where is the mass transfer coefficient, is the particle diameter, is the diffusivity, is the Reynolds number calculated using the superficial velocity through the bed, is the Schmidt number, and is the bed void fraction.
- Mass transfer between vapor and liquid in an agitated vessel can be described by the Van't Riet equations:
- For air-water:
- and for air-water-electrolyte:
- where is the mass transfer coefficient, is the interfacial area per unit volume, is the gas volumetric flow rate, is the liquid volume, and is the agitator power input.
- Fair's method for calculating the mass transfer coefficient for low viscosity systems is given by:
- where is the liquid phase diffusivity.
- Mass transfer correlations for vapor-liquid systems should be used with caution when there are surfactants (Towler and Sinnott, 2013).
Step 2: Select Reaction Conditions
A major determining factor in reactor type selection is the choice of operating conditions. Optimal process operation usually involves optimizing process yield and not necessarily reactor yield. Based on the preliminary economical analysis a target range of yields and selectivities can be chosen. The final reaction conditions must be verified experimentally to ensure target yields and selectitivities are realized (Towler and Sinnott, 2013).
Chemical or Biochemical Reaction
If the desired product is to be produced by a biochemical reaction the chosen conditions must maintain the viability of the biological agent (e.g. microorganisms or enzymes). Proteins denature outside of their specific temperature and pH ranges, while living organisms require specific concentrations of oxygen and other solutes to survive and cannot withstand high shear rates. See bioreactors for further information on their design.
Catalyst
A catalyst is used to increase the reaction rate by lowering the activation energy without being consumed in the reaction. The use of catalyst imposes operating condition constraints as the catalyst must maintain activity for a period of time between catalyst regenerations. Catalyst deactivation can be accelerated by high temperatures as well as contaminants in the feed or recycle streams.
Temperature
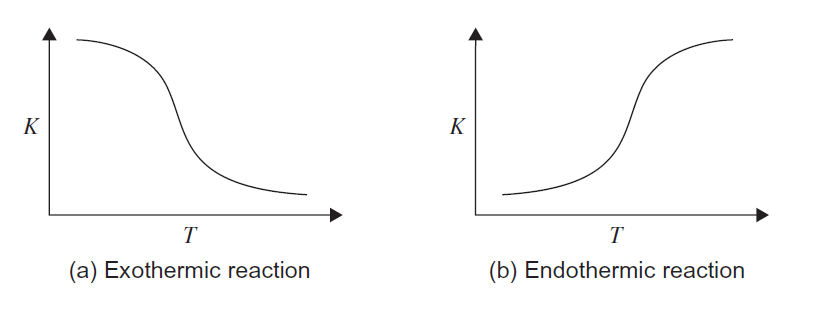
Increasing the reaction temperature will increase the reaction rate, diffusivities, and mass-transfer rates. Temperature also affects the equilibrium constant: higher temperature increases equilibrium constant for endothermic reactions and decreases it for exothermic reaction- see the figure below.
- Figure 2. Effect of temperature on equilibrium constant (Towler and Sinnott, 2013)
Increased reaction temperature will reduce the cost of reactor design except for the following scenarios/considerations (Towler and Sinnott, 2013):
- Biochemical reactions where living organisms could die at high temperatures
- Presence of organic compounds that undergo thermal degradation
- Unwanted side reactions that accelerate with higher temperature, such as polymerization or auto-oxidation
- Oxidation reactions where selectivity decreases at higher temperatures as product oxidation tends to increase
- Exothermic reactions as it is more difficult to control the temperature and there is risk of reaction run away
- Construction cost of the reactor can become prohibitive at extremely high temperatures
Pressure
The main consideration when choosing the reactor pressure is to maintain the reaction at the desired phase for the selected temperature. The pressure can also be chosen to allow for vaporization of a component, making separation of a product easier, shifting the reaction equilibrium, or removing heat from the reactor. Increasing pressure for reactions that take place in the gas phase increases reactant activity and thus the reaction rate. Reactor yields follow Le Chatelier's principle: for reactions that increase number of moles lower pressure will increase equilibrium conversion, for reactions that decrease number of moles lower pressure will decrease equilibrium conversion. Increasing the pressure in gas-liquid reactions increases the solubility of the gas in the liquid which increases the reaction rate.
Reaction Phase
Reactions are usually carried out in liquid or gas phases as fluids are easier to handle, heat and cool, and transport than solids. For reagents or products in the solid phase a suspension in liquid or gas is usually used. The phase of the reaction is usually determined by reactor temperature and pressure. Liquid-phase operation is usually preferred due to the highest concentrations and greatest compactness. However, at temperatures above the critical temperature there cannot be a liquid phase. The pressure can sometimes be adjusted to keep all reagents in the liquid phase, however when this is not possible a multiphase reactor will be necessary. If mass transfer limitations become too significant it can be beneficial to reduce the pressure such that the reaction temperature is above the dew point and the reaction is carried out in the vapor phase.
Solvent
Solvents are used for liquid-phase reactions and can be used for the following:
- Dilution of feed to improve selectivity
- Increasing solubility of gas-phase components
- Dissolving solids in the reacting phase
- Increasing thermal mass which lowers temperature change per unit volume from reaction
- Improving miscibility of mutually insoluble components
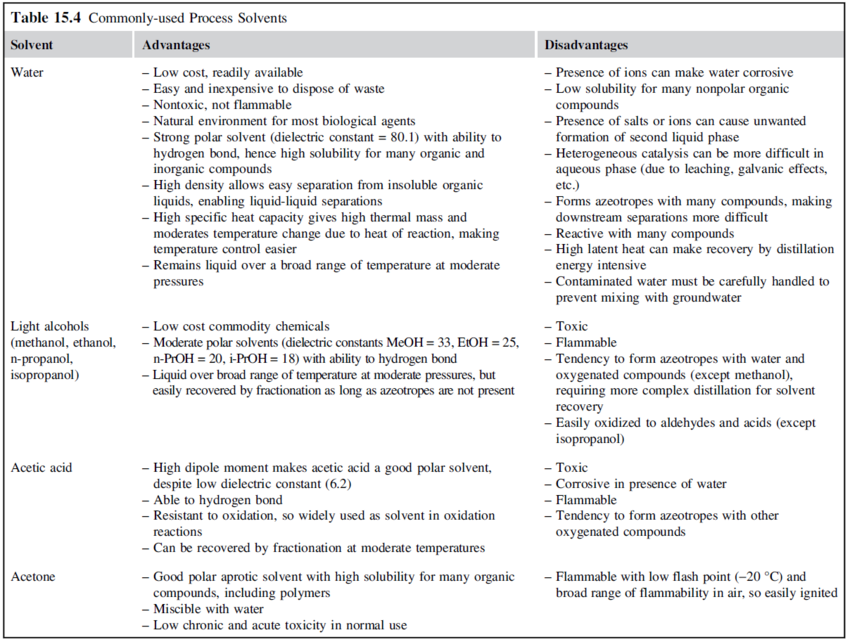
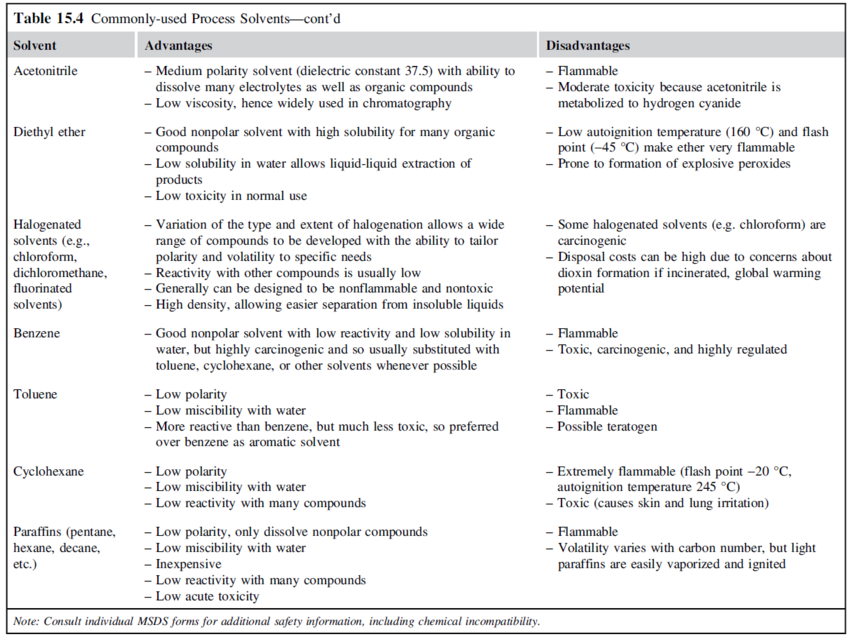
Solvents should be inert in the main reaction and should not react with products or feed contaminants. Solvents should also be inexpensive and easily separated from the reaction products. Some widely used process solvents and their properties are given in the table below:
- Commonly used process solvents (Towler and Sinnott, 2013)
Concentrations
Higher concentrations of feed can lead to higher reaction rate, however for exothermic reactions high feed concentrations should be avoided. Feed compounds are usually not supplied in stoichiometric ratio as using a higher concentration of one feed can lead to increased selectivity towards the desired product.
Understanding the effect of feed contaminants and by-products is essential to reactor design; they can play significant roles in reactor selectivity and performance. When recycling attention must be paid to by-products; those formed through reversible reactions can be recycled leading to improved overall selectivity. Feed contaminants generally pose a greater issue than by-products due to their ability to poison catalysts or kill biological organisms. If a feed contaminant is particularly detrimental to the reactor performance it should be removed upstream of the reactor.
Inert compounds will usually increase reactor cost due to the larger volume required, as well as increase downstream separation costs; they can still be advantageous for the following circumstances:
- Inerts in gas-phase reactions reduce partial pressure of reagents which can increase equilibrium conversion in reactions that lead to an increase in number of moles
- Feed compound reacting with itself or products can be reduced by dilution using inerts
- Inerts can allow operation outside of the flammability envelope
- Reaction solutions can be buffered to control pH
Step 3: Determine Materials of Construction
A preliminary analysis of the materials of construction for the reactor can be conducted after the reaction conditions have been specified. Particularly important in this analysis are the temperatures and pressures the process will run at. At extreme conditions, costly alloys may need to be used. In addition, the designer must ensure that process streams will not react with materials used in process equipment.
Step 4: Determine Rate-Limiting Step and Critical Sizing Parameters
The key parameters that determine the extent of reaction must be identified by carrying out an experiment plan with a broad range of conditions. In general, the rate of reaction is usually limited by the following fundamental processes. The first three have been discussed in previous sections. Mixing will be developed in more detail in its own section.
- Intrinsic kinetics: There will usually be one slowest step that governs the overall rate.
- Mass-transfer rate: In multiphase reactions and processes that use porous heterogeneous catalysis, mass transfer can be particularly important. Often, careful experimentation will be needed to separate the effects of mass transfer and the rate of reaction to determine which is the rate-limiting step.
- Heat-transfer rate: The rate of heat addition can become the governing parameter for endothermic reactions. Heat-transfer devices such as heat exchangers or fired heaters may need to be used.
- Mixing: The time taken to mix the reagents can be the limiting step for very fast reactions.
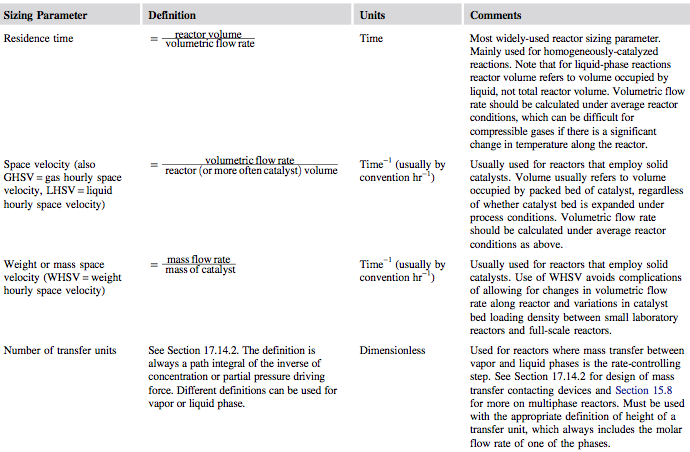
Once rate data have been collected, the designer can fit a suitable model of reaction kinetics. Next, a critical sizing parameter can be specified for the reactor. This will usually be one of the parameters given in Figure 1.
- Figure 1. Reactor Sizing Parameters (Towler and Sinnott, 2013)
Step 5: Preliminary Sizing, Layout, and Costing of Reactor
The designer can estimate the reactor and catalyst volume from the sizing parameter. This calculation will yield a value for the active reacting volume necessary. Clearly, the actual reactor will need additional space. The geometry of the reactor will depend on the desired flow pattern and mixing requirements (Towler and Sinnott, 2013). The cost of most reactors can be estimated by determining the cost of a pressure vessel with the same dimensions and adding in the cost of the internals (Towler and Sinnott, 2013).
Step 6: Estimate Reactor Performance
At this point in the design process, it is important to verify that the proposed reactor will achieve the target conversions and selectivities. A combination of experimental methods, such as pilot plants, and computer simulations can be used to predict the full-scale reactor performance.
Step 7: Optimize the Design
The reactor is typically a relatively small fraction of the total capital cost (Towler and Sinnott, 2013), so minimal time should be devoted to optimization to reduce the reactor cost. However, if the target conversion, yields, and selectivities are not met, the process economics could be significantly impacted. Therefore, steps 2 to 6 should be repeated at least until the minimum specifications are met (Towler and Sinnott, 2013).
Mixing in Industrial Reactors
Mixing plays an important role in many processing stages, including reactor performance. It is critical to select the appropriate method of mixing in order to ensure the process produces the desired process yields, product purity, and cost effectiveness.
Correlations such as the Reynolds number can be used to determine the extent of mixing and correlate power consumption and heat transfer to the reactor shell (Towler, 2012). In some cases, simple correlations may not be adequate:
- If dead zones cannot be tolerated for reasons of product purity, safety, etc.
- If reactor internals are complex
- If reaction selectivity is very sensitive to mixing
In these cases, it is usually necessary to carry out a more sophisticated analysis of mixing:
- Use computational fluid dynamics to model the reactor
- Use physical modeling (“cold flow”) experiments
- Use tomography methods to look at performance of real reactor
Gas Mixing
Gases mix easily because of their low viscosities. The mixing given by turbulent flow in a length of pipe is usually sufficient for most purposes (Towler and Sinnott, 2013). Orifices, vanes, and baffles can be used to increase turbulence.
Liquid Mixing
- Inline Mixing Inline mixers can be used for the continuous mixing of low-viscosity fluids. One inexpensive method involves the use of static devices that promote turbulent mixing in pipelines. Some typical designs are shown in Figures 2(a), (b), and (c).
- Figure 2. Inline mixers: (a) tee; (b) injection; (c) annular (Towler and Sinnott, 2013)
- When mixing low viscosity fluids (<50 mNs/m2) with similar densities and flow rates, a simple mixing tee, Figure 2(a), followed by a length of pipe equal to 10 to 20 pipe diameters, is suitable (Towler and Sinnott, 2013).
- When one flow is much lower than the other, an injection mixer, Figure 2(b&c), should be used. A satisfactory blend will be achieved in about 80 pipe diameters (Towler and Sinnott, 2013). Baffles or other flow restrictions can be used to reduce the mixing length required. These mixers work by introducing one fluid into the flowing stream of the other through a concentric pipe or an annular array of jets (Towler and Sinnott, 2013).
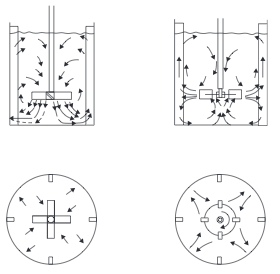
- Stirred Tanks Stirred tanks were discussed in the Ideal Reactors section. Mixing is conducted by an impeller mounted on a shaft driven by a motor. The reactor usually contains baffles or other internals to induce turbulence and prevent the contents from swirling and creating a vortex. Typically, baffles are 1/10 of diameter and located 1/20 of diameter from wall (Towler, 2012). A typical arrangement of agitator and baffles in a stirred tank, and the flow pattern generated, is shown in Figure 3. Mixing occurs through the bulk flow of the liquid and by the motion of the turbulent eddies created by the agitator. Bulk flow is the predominant mixing mechanism required for the blending of miscible liquids and for solids suspension. Turbulent mixing is important in operations involving mass and heat transfer, which can be considered as shear-controlled processes (Towler and Sinnott, 2013).
- Figure 3. Agitator arrangements and flow patterns (Towler and Sinnott, 2013)
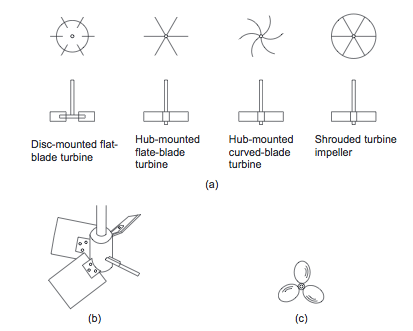
- At high Reynolds numbers (low viscosity), one of the three basic types of impeller shown in Figure 4 should be used. For processes controlled by turbulent mixing, the flat-bladed (Rushton) turbines are appropriate. For bulk mixing, the propeller and pitched-bladed turbines are appropriate (Towler and Sinnott, 2013).
- Figure 4. Basic impeller types (Towler and Sinnott, 2013)
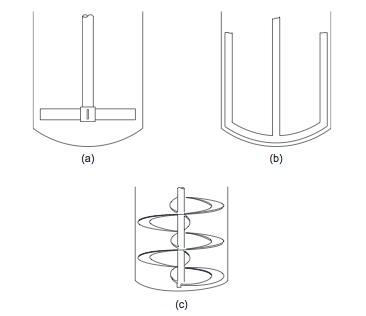
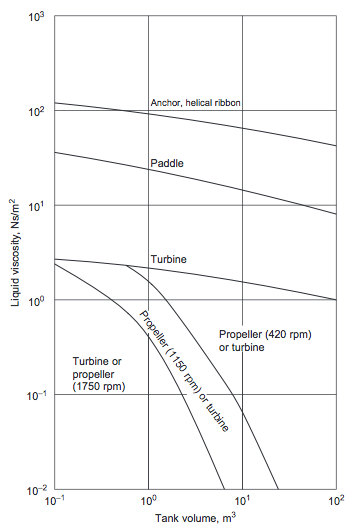
- For more viscous fluids, paddle, anchor, and helical ribbon agitators (Figures 5(a), (b), and (c)), are used (Towler and Sinnott, 2013). The selection chart given in Figure 6 can be used to make a preliminary selection of the agitator type, based on the liquid viscosity and tank volume (Towler and Sinnott, 2013).
- Figure 5. Low-speed agitators (Towler and Sinnott, 2013)
- Figure 6. Agitator selection guide (Towler and Sinnott, 2013)
Gas-Liquid Mixing
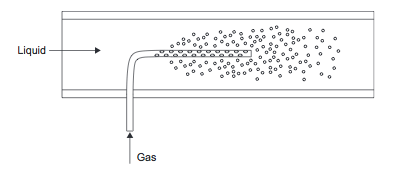
Gases can be mixed into liquids using the inline mixing or stirred tank methods discussed previously. A special type of gas injector, called a sparger (shown in Figure 7) can also be used. This is a long injection tube with multiple holes drilled in it.
Figure 7. Gas sparger (Towler and Sinnott, 2013)
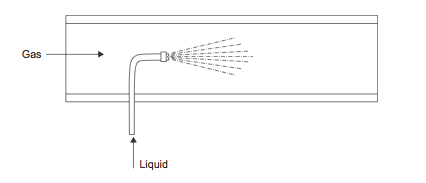
A small flow of liquid can be dispersed into a gas stream using a spray nozzle (Figure 8).
Figure 8. Liquid injection into gas (Towler and Sinnott, 2013)
Solid-Liquid Mixing
Solids are usually added to a liquid in a stirred tank at atmospheric pressure. In order to allow more accurate control of dissolved solid concentration, mixing of solids and liquids is often carried out as a batch operation (Towler and Sinnott, 2013).
Types of Reactors
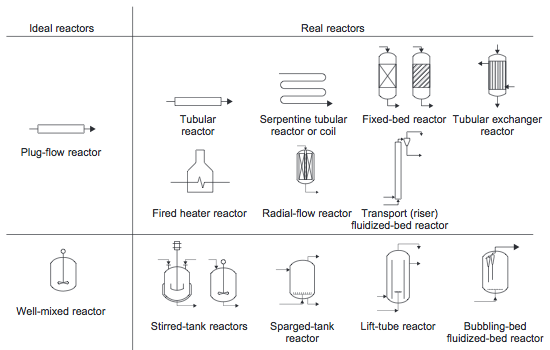
Most reactors used in industry approximate the ideal batch reactor, PFR, or CSTR. In fact, real reactors can be modeled as networks or combinations of multiple plug-flow and stirred-tank reactors (Towler and Sinnott, 2013). Examples of real reactors that approximate the flow pattern of ideal reactors are shown in Figure 10. These reactors will be discussed in more detail in the following sections.
Figure 10. Ideal reactors and some real reactors that approximate the same flow pattern (Towler and Sinnott, 2013)
Vapor-Liquid Reactors
Vapor-liquid reactions are important in many chemical processes. For example, oxygenation and hydrogenation reactions are usually carried out with the organic component in the liquid phase (Towler and Sinnott, 2013). A summary of common goals for vapor-liquid reactors and the reactors used to achieve those goals is shown in Table 1.
| Goal | Types of Vapor-Liquid Reactors | Examples |
|---|---|---|
| Maintain low concentration of gas component in liquid |
|
|
| Contact gas and liquid over catalyst |
|
|
| React a component out of the gas phase to high conversion |
|
|
Table 1. Summary of Vapor-Liquid Reactors (Towler, 2012)
If the residence time requirements are short enough, vapor-liquid contacting columns are preferred because of the high area for mass transfer. Trayed or packed columns can be used to contact vapor and liquid for reaction. The column packing may be catalytically active or could be inert packing (Towler, 2012). Please see the separation processes section of this website for more information on the types of processes used for the third goal listed.
Stirred tanks or tubular reactors are used when long residence time is needed for the liquid phase (Towler and Sinnott, 2013). These types of reactors and more will be discussed in the catalytic processes section of this page.
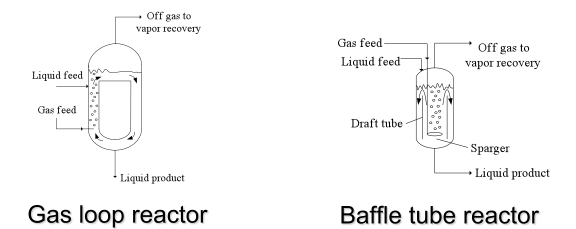
The reactors listed under the first goal in the table are unique to vapor-liquid processes. The basic concept of a sparger was discussed in the mixing section. Sparged reactors are shown in Figure 11.
Figure 11. Sparged stirred tank and tubular reactors (Towler, 2012)
The gas is bubbled up through the liquid in a sparged reactor. For smaller bubbles, a porous pipe diffuser can be used instead (Towler, 2012). The designer must allow some disengaging space at the top of the reactor, or entrainment will be excessive. If the gas flow rate is large then the gas flow can be used as the primary means of agitation. Perry's Handbook suggests the following air rates (ft3/ft2min) for agitating an open tank full of water at 1 atm:
| Degree of agitation | Liquid depth 9 ft | Liquid depth 3 ft |
|---|---|---|
| Moderate | 0.65 | 1.3 |
| Complete | 1.3 | 2.6 |
| Violent | 3.1 | 6.2 |
Table 2. Summary of suggested flow rates for gas flow as agitation (Towler, 2012)
Catalytic Processes
A catalyst increases the rate of a chemical reaction without itself becoming permanently changed by the reaction. Catalysts allow reactions to be run in smaller reactors and operated at lower temperatures and improve selectivity. Therefore, catalysts will almost always lead to a more economically attractive process than a noncatalytic route (Towler and Sinnott, 2013). Catalysts are normally selected based on performance rather than price since increases catalysts selectivity will almost always quickly pay back any price premium expected by the manufacturer. It is important to test the catalysts under conditions that are representative of process conditions (Towler and Sinnott, 2013).
Catalyst activity often deteriorates over time (Towler, 2012). Common causes of deactivation include:
- Poisoning by components in feed (e.g. base destroys acid catalyst)
- Blockage of pores or active sites by byproducts such as coke
- Thermal or hydrothermal modification of catalyst structure
Slow activity loss can be compensated by:
- Putting in more catalyst (lower space velocity)
- Slowly raising reactor temperature
Rapid activity loss may require moving the catalyst to a continuous regeneration zone (Towler, 2012).
Catalytic reactions can be either homogenous (catalyst is in the same phase as the reagents) or heterogeneous (catalyst is not in the same phase as the reagents).
Homogeneous Catalysis
- Homogeneous catalysis can be conducted in the basic batch reactors, PFRs, or CSTRs that have already been discussed. However, when the catalyst is in the same phase as the reagent, recovering this catalyst after the reaction can be difficult and expensive, particularly if the catalyst is sensitive to high temperatures (Towler, 2012). Providing adequate interfacial area is also a challenge of homogeneous catalysis. A reaction often only occurs at the interface or in the boundary layer between the catalyst and the reagents. Increased mixing can increase the rate and selectivity of the reaction, but this can require detailed and expensive mixing equipment (Towler, 2012). For these reasons, reactions requiring homogenous catalysts are not usually used unless an easy separation can be found to recover the catalyst.
Heterogeneous Catalysis
- Catalyst recovery in processes involving heterogeneous catalysis is much easier. However, the rate of reaction is limited by the available inter-phase surface area and the mass transfer of reagents and products to and from the interface (Towler, 2012). Therefore, reactors for these processes are design to reduce these limitations.
- Fixed Bed Reactors
- In a fixed-bed reactor, the reagent flows over a stationary bed of packed catalyst (Towler and Sinnott, 2013). This is the most common type of reactor used for heterogeneous catalysis as long as the catalyst does not require continuous regeneration and the reaction mixture does not require high agitation (Towler, 2012). The amount of catalyst necessary can be found using the following equations:
- The ratio of the bed height (L) to the diameter (D) determines the distribution of reagents and the pressure drop across the bed. An increased L/D ratio creates a more even distribution and less change of localized deactivation or "hot spots." However, increasing the L/D ratio increases the pressure drop, requiring higher compression and pumping costs (Towler, 2012). The Ergun equation can be used to calculate the pressure drop in packed beds.
- Where V is the superficial velocity (volume flowrate divided by cross-sectional area), μ is the viscosity, Dp is the particle diameter and ε is the porosity of the packed bed (Towler, 2012). Given these trade-offs, it may make sense to split the catalyst over several beds (Towler, 2012).
- Radial Flow Reactors
- When there is very little pressure drop available, the L/D ratio must be much less that one (Towler, 2012). A common solution to this is to use a radial flow reactor with the catalyst contained in an annulus between vertical perforated or slotted screens. The fluid flows radially through the bed and the direction of flow can be either inwards or outwards (Towler and Sinnott, 2013). An example of a radial flow reactor is shown in Figure 12.
- Figure 12. Radial flow reactor (Towler, 2012)
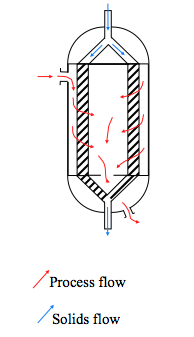
- Moving Bed Reactors
- A moving bed reactor is similar to a radial flow reactor, but the catalyst is moved through the annular space (Towler, 2012).
- Fluidized Bed Reactors
- If the fluid flow is up through the catalyst bed then the bed can become fluidized if the pressure drop is high enough to support the weight of the catalyst. Fluidized beds usually have a lower pressure drop than down flow at high flow rates (Towler, 2012). In addition, fluidizing the catalyst eases the transition from one reaction zone to another.
- The catalyst bed is fluidized using a distributor to inject fluidization fluid, which is not necessarily the feed. Fluidization occurs when the bed pressure drop balances the weight of the particles, or
- Where ∆P is the pressure drop, ρp and ρg are the densities of the particle and gas respectively, εm is the porosity at minimum fluidization, and L is the height of the bed (Towler, 2012). Fluidization can only be used with relatively small sized particles (<300 micrometers with gases). The solid material must be strong enough to withstand attrition in the fluidized bed and cheap enough to allow for make-up to replace attrition losses (Towler and Sinnott, 2013). A fluidized-bed reactors must also make allowance for separating the fluid-phase product from entrained solids so that solids are not carried out of the reactor (Towler and Sinnott, 2013).
- Trickle Bed Reactors
- Trickle bed reactors are used when all three phases are involved in the reaction. They must ensure good distribution of both the vapor and the liquid, without channeling of either phase (Towler, 2012). In a trickle bed reactor, the liquid flows down over the surface of a stationary bed of solids. The gas phase usually also flows downwards with the liquid, but countercurrent flow is feasible as long as flooding conditions are avoided (Towler and Sinnott, 2013). This requires a more sophisticated distributor like those used for packed distillation columns (Towler, 2012). An example of a trickle bed reactor is shown in Figure 13.
- Figure 13. Example of trickle bed reactor (Towler, 2012)
- Slurry Reactors
- Liquid is mixed up in the liquid in slurry phase reactions. Slurry reactors are prone to attrition of the solids, caused by pumping or agitation of the liquid (Towler and Sinnott, 2013). Slurry-phase operation is usually not preferred for processes that use heterogeneous catalysts because the catalyst tends to become eroded and can be difficult to recover from the liquid (Towler and Sinnott, 2013).
Bioreactors
Bioreactors have requirements that add complexity compared to simpler chemical reactors. These reactions often are three-phase (cells, water, and air), need sterile operation, and require heat removal (Towler, 2012). However, biological systems have the following advantages:
- Some products can only be made by biological routes
- Large molecules such as proteins can be made
- Selectivity for desired product can be very high
- Products are often very valuable
Enzyme Catalysis
Enzymes are the biological equivalent of catalysts. They can sometimes be isolated from host cells. They are usually proteins and, therefore, most are thermally unstable above ~60 degrees Celsius and active only in water at a restricted pH (Towler, 2012). Enzymes can sometimes be absorbed onto a solid or encapsulated in a gel without losing their structure. In this case, they can be used in a conventional fixed bed reactor. Typically, homogenous reactions are carried out in batch reactors.
Microorganism Design and Selection
As an alternative to an enzyme catalyst, engineered microorganisms can be used to produce a chemical of interest. This product could be complex biological compounds, therapeutic proteins, or commodity plastics and fuels (Westfall 2011). Host cells as a platform for modification have so far included bacteria, yeast, and mammalian cells (Schmidt 2005). The efficiency of a bioreactor is heavily dependent on the efficiency of the microorganism used. An inefficient cell host that does a poor job of producing the desired product will always result in a poorly designed bioreactor, regardless of the equipment or conditions used. Furthermore, the design of a bioreactor is largely based around the ideal growth conditions of the microorganism. As shown in this section, the design and/or selection of a microbial host is closely related to the design of the bioreactor. Choice of a host demands particular reactor conditions, and in the case of genetically engineered microbes, the cells must be designed to operate in conditions that are feasible and affordable with modern bioreactor technology. This process can involve the rigorous engineering of a novel microorganism, a large screening for high producing strains, or, most likely, a combination of the two. This step of the bioreactor design process requires close collaboration between process engineering and microbiology.
Fermentation Goals
Fermentation as a general practice is carried out with the following goals, many of which are effected directly by microorganism choice (Shuler 2002).
Cost, Yield, and Productivity
The goal of an efficient microbial host results in four parameters that relate microbe performance to the overall reactor performance. Overall fermentation performance for batch and fed batch processes can be evaluated as
where represents the concentration of desired product, the concentration of cells, and the specific productivity in mass of product per mass of cells per time. Cell growth can be modeled by the equation
where is the specific growth rate per time. Desirable values for these parameters for a scaled bacterial process are a productivity of 0.1 g/L-hr and a growth rate of 0.2-0.7 1/hr. As discusses later, these parameters are specific to cell lines, and are difficult to engineer orthogonally.
In addition to growth and product formation, it is important to consider substrate consumption in selecting an efficient microorganism. Often high product titers can be obtained with excessive waste of substrate, leading to extensive costs and unrealistic reactor sizes. In order to best understand substrate utilization, it is easiest to view the composition of the organism and the product as a whole to develop substrate requirements, shown in the following tables.
While many elements are required, it is not necessary to model all of them. For evaluating the consumption of feed, it is useful to model the organism's chemical consumption on an elemental level for only the first four.
where w,x,y,z indicate substrate composition, r,s,t indicate the relative cell composition, and j,k,l,m indicate the composition of the product. Alone, this design equation cannot be solved for a single solution. Instead, two additional parameters are required that are specific to the cell host. and represent the yield of cell mass and product mass per mass of fed substrate. These parameters characterize how the cell host utilizes its feed, and again are difficult to orthogonally engineer. Using this stoichiometric design equation and a desired product formation rate, the rate of substrate utilization can be calculated. In this way, the overall fermentation yield relies heavily on these four organism design parameters, and .
For continuous fermentation, the process holds the same dependence on these parameters, which are found in the following design mass balance.
Product Isolation and Purification
Downstream processing of the product is primarily dependent on the nature and chemical properties of the product itself. For example, a particular intracellular protein may be very difficult to separate from other cell internals. However, the choice of microorganism can have a significant impact on early separation steps, specifically the separation of the product from the cell mass. Paramount is whether or not the product is excreted from cells. Bacteria like E. coli lack many of the mechanisms required to excrete a desired product into the fermentation broth. This requires the lysing of cells in early downstream processing and separation of the product from cell internals. This process would be executed in batches, which can be timed optimally to maximize use of fermentation and separation equipment (Biegler 1997). On the other hand, mammalian cells and yeast can be engineered or screened to secrete the product of interest into the fermentation broth. This process removes the requirement of lysis step, and greatly simplifies the purification of product. This also makes the reactor particularly amenable to continuous fermentation (Huang 2008). Additionally, eukaryotic cells can produce more complex products, such as glycosylated protein. The glycosylation of proteins is a mechanism only recently achieved in bacteria (Nothaft, 2010).The table below indicates advantages and disadvantages of different types of organisms.
Operation Conditions, Equipment, and Scale Up
It is important for the process engineer to select a microorganism that can operate within reasonable reactor conditions.
- Feed: The microbe must exhibit desirable design parameters when grown on a feed that is not commercially or cost restrictive. Below are several common bioreactor feeds.
- Heat: The microbe must exhibit desirable design parameters at a temperature that is reasonable to maintain in a bioreactor. Because fermentation generates excessive heat from substrate breakdown, this generally involves cooling the reactor to between ambient and 37 C (Towler 2012). A microbial host that requires temperatures too high or low is not amenable to a controlled fermentation. This is especially salient with extremophiles - microbes that live in extreme conditions that often exhibit naturally high titers of high value products. In this case, it would be necessary to engineer the extremophile, or choose a more reasonable cell host.
- Oxygen: Microbes can generally grow in aerobic or anearobic conditions. Often, product formation and growth will be favorable in aerobic conditions. If this is the case, it is important to consider the oxygen requirement to maintain aerobic conditions, and ensure that the bioreactor designed can meet the requirements of the organism at the desired growth rates and concentrations. When designing a microorganism, it is important to not require an oxygen usage rate that is above what a reasonable bioreactor can provide.
Challenges in Microorganism Design
Cells must be engineered to produce a heterologous product through recombinant DNA. For a therapeutic protein, this includes identifying the DNA sequence coding for the protein, and expressing that DNA in a cell host (Seider 2004). For a commodity molecule, enzymes that catalyze the synthesis of that molecule must be identified and expressed in the host cell. The engineering of microorganisms presents a number of formidable challenges. Many companies avoid this issue by screening known microorganisms for strains that naturally produce high titers of product, or close precursors. Expressing heterologous genes in cells causes high stress, and disrupts natural metabolic balance.
There are many techniques used for the engineering of microorganisms. These involved mostly the manipulation and delivery of heterologous DNA to the host cell line, to genetically manipulate its phenotype. However, because this wiki focuses on design for the process engineer, those techniques are left out of this discussion. Instead, the aspects of organism design that impact the process parameters exhibited by the organism will be elucidated. This mainly involves balancing the observed and to maintain high productivity and growth rate.
Metabolic engineering studies ways to relieve these stresses by “rewiring” synthesis networks within cells (Stephanopoulos 1998). This includes largely two parts. The first involves constructing non-native biochemical pathways in cells. This is necessary if the host does not already produce the desired product. Enzymes are expressed in the host that catalyze the correct reactions to synthesize the product. This often puts stress on cells, as it diverts resources in the cell towards the product that are typically utilized elsewhere, such as for growth. The second aspect of metabolic engineering involves the manipulation and balancing of metabolic fluxes within the cell. This involves controlling the expression of enzymes so that the cell makes enough product, but still has enough resources to grow to an acceptable level. Sometimes, it can be advantageous to only induce production of the product after cells have grown to a high concentration. This requires the heterologous DNA to be expressed with an inducible promoter. For example, production of a product could be induced when the feedstock is switched to methanol (Yurimoto 2000).
A parallel strategy to metabolic engineering is protein engineering. This simply involves the design or random testing of proteins, usually enzymes, to either enhance or alter their function. This is used in conjunction with metabolic engineering to either create novel pathways, or balance existing pathways.
Case Studies
In this section, two case studies are considered. The production of penicillin stands as the first high profile selection of an industrial microorganism. The more modern production of artemisinin from bacteria serves as a canonical example of microorganism design.
Penicillin Production
In 1928, Alexander Fleming discovered that the mold Penicillium notatum produced a substance that would kill bacteria. The product was named penicillin, and was not studied for nearly 10 years. With the advent of World War II, the demand of effective antibiotics cause penicillin to be characterized. It was purified for study by biochemists, and found to be extremely effective. There now existed a demand for the mass production of the drug, which at that time had traditionally been done by chemical synthesis. However, the fragility and complexity of penicillin forced American pharmaceutical companies to pursue a fermentation process, taking advantage of the biological mechanisms already in place for the molecule's production. Designing this novel industrial process including two major challenges, both related to the selection of the optimal microorganism. First, the product was produced at low amounts, and increased product concentrations were necessary for industrial production. Second, the organism had to perform at a repeatable, characterizable, level on large scales with large, often anaerobic tanks. Hundreds of Penicillium strains were isolated and characterized, with Penicillium chrysogenum being selected, which produced penicillin at two orders of magnitude higher than other tested strains. This allowed a product concentration of 0.001 g/L in scaled bioreactors. This number is extremely low by today's standards, and presented a formidable purification challenge. Purification was assisted by the excretion of penicillin by the mold, a major advantage of eukaryotic fermentation. Today, after countless iterations of strain modification, product concentrations exceed 50 g/L (Shuler 2002).
Artemisinin Production
Artemisinin is an effective anti-malarial drug, and is the treatment of choice for the Plasmodium falciparum parasite. Up until a decade ago, access to this important drug was limited in several parts of the world. Since then, bioengineers have successfully designed microorganisms that can produce artemisinin at levels high enough to provide significant increases in worldwide accessibility.
Artemisinin is derived from the herb Artemisia annua. Unfortunately, it is produced in trace levels in the plant. Purification is difficult and requires impossible amount of plant biomass. Efforts made to engineer the natural pathway of artemisinin synthesis have been met with little success. The synthesis pathway of artemisinin in vivo is largely unknown. While the genetic manipulation of the expression of several enzymes has increased yields, the production is not at a level amenable to a bioreactor. In parallel, strategies to produce artemisinin through chemical synthesis or biochemical pathways in vitro have met similar challenges.
Success in artemisinin production has come in the form of engineered microorganisms. The highest production titers to date are the result of the heterologous expression of enzyme pathways from plants in both the bacteria Escherichia coli and the yeast Saccharomyces cerevisiae, with E. coli seeing more success. Currently, E. coli can achieve 450 mg/L of product after 60 hours, and S. cerevisiae can achieve 153 mg/L over 16 days. These successes were met using three techniques. First, metabolic pathways for artemisinin precursors were assembled in the microorganisms from a number of sources. Second, several enzymes were mutated to improve or slightly alter their function. Third, gene expression of each enzyme was tuned to optimize the amount of enzyme needed for each synthetic step. These techniques allowed the productivity of the cells to remain high while retaining a stable growth rate. Microorganisms that exhibit this balance of cell yield and product yield are ideal for bioreactors (Arsenault 2010).
Cell Growth
Cell growth goes through several phases during a batch, shown in Figure 15.
Figure 15. Cell growth and product formation in batch fermentation (Towler and Sinnott, 2013)
- I: Innoculation: slow growth while cells adapt to new environment
- II: Exponential growth: growth rate proportional to cell mass
- III: Slow growth as substrate or other factors begin to limit rate
- IV: Stationary phase: cell growth rate and death rate are equal
- V: Decline phase: cells die or sporulate, often caused by product build-up
Innoculation
The Innoculation, or Lag phase is the first step of cell growth during a batch fermentation process. There is a minimal increase in cell density. This phase is least understood by scientists but has been noticed since the end of the 19th century. There is a lack of data that can adequately explain the physiological and molecular processes that take place during this phase.
Exponential Growth
The exponential phase, also known as the logarithmic growth phase, occurs when cells adjust to their new conditions. They are diving at a constant rate resulting in an exponential increase in cells following first order kinetics. The equation below illustrates this process:
Cell growth is often substrate limited, meaning the growth will plateau once substrates become less available. Cell growth rate can be measured by different forms of inhibition. These forms include substrate inhibition, product inhibition, and toxic compounds inhibition.
Stationary Phase
Stationary phase occurs when the number of cells dying and dividing reaches an equilibrium. This can be caused due to the depletion of one or more growth nutrients, the accumulation of toxic byproducts, the induction of a gene. Induction causes a stressful environment for cells and increases the death rate. In this phase, production of the primary metabolite stops, but the production of a secondary metabolite can continue.
Decline Phase
The decline, or death phase occurs when the rate of cell death is greater than of cell generation. It is represented by the following first order kinetics equation:
Measuring Growth
One easy way to quickly establish a growth curve is to measure the optical density with a spectrophotometer. A sample of the fermentation liquid is taken up and the absorbance of the sample is measured with the spectrophotometer. The measured value is then combined with previous measurements and a curve can be constructed. One drawback of this method is that both viable and non-viable cells are measured and taken into account.
Intracellular product accumulation is slow at first because there are a limited number of cells (Towler, 2012). However, it is important to note that product accumulation continue even after the live cell count falls, since dead cells still contain product.
The growth rate of cells can be limited by factors such as:
- The availability of the primary subtrate
- Typically glucose, fructose, sucrose, or other carbohydrate
- The availability of other metabolites
- Vitamins, minerals, hormones, or enzyme cofactors
- The availability of oxygen
- Mass transfer properties of the reaction system
- Inhibition or poisoning by products or byproducts
- High temperature caused by inadequate heat removal
All of these factors are exacerbated at higher cell concentrations (Towler, 2012). Clearly, biological reactions must be carefully controlled. An addition complication in dealing with biological reactions is that the product formation is often not closedly tied to the rate of consumption of the substrate (Towler, 2012). This is because of the fact that the product may be made by the cells at a relatively low concentration and the fact that some cell metabolic processes may not be involved in formation of the desired product (Towler, 2012).
Batch or Continuous
Batch
Batch bioreactors represent the majority of industrial processes. This requires a sterilization phase and inoculation of the culture medium with microorganisms before the reaction can occur. Some advantages of batch systems include (William, 2002):
- A reduced risk of contamination due to a short growth time
- Lower capital investment
- More flexibility for biological systems
Some disadvantages include:
- Intermediate steps that cause decreased productivity levels
- High expense when preparing culture for inoculation
- Higher hygiene risks due to close contact with microorganisms
Continuous
For a continuous process, media that is either sterile or contains bacteria is continuously fed into a bioreactor in order to hold the steady state. Some advantages of continuous systems include (William, 2002):
- Potential for automation
- Lower costs of labor
- Less time spent sterilizing and preparing
- Consistent product quality
Some disadvantages include:
- Only small changes in process are allowed
- Feed quality needs to be specified and maintained
- Higher investment costs
- Risk of cell mutation due to short cultivation
Case Study: Batch vs Continuous
A research group compared the rates of production of the enzyme xylanase. Filamentous fungi secrete this enzyme into the medium during fermentation and have much higher activity than yeast and bacteria. This enzyme increases the body weight gains of animals. It is also used in prebleaching in the paper industry as well as helps regulate dough viscosity in the baking industry. Finally, it can be used for the production of fuel and chemical feedstocks (Bakri, 2012).
Due to the nature of continuous condition, the group predicted that this option should yield higher results. Continuous fermentation does not require time to clean up and sterilize new batches. The cells were grown in a 3 liter Electro-lab fermenter with a barley straw hydrolase medium. For the batch portion of the experiment, the reactor was filled with 1.5 liters of medium and was inoculated with a concentration of a million spores per milliliter. For the continous portion of the experiment, the medium was pumped into the bioreactor using a peristaltic pump at a speed of 75 milliliters per hour. The speed was chosen to allow for the retention of 1.5 liters of culture during the process (Bakri, 2012).
The results for both batch and continuous methods are illustrated below:
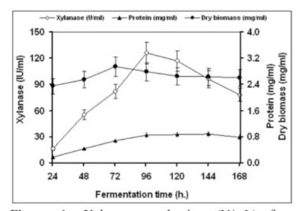 Figure 16: Xylanase production using batch method
Figure 16: Xylanase production using batch method
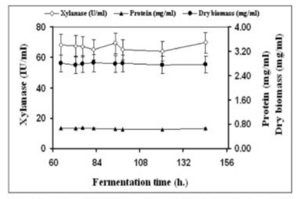 Figure 17: Xylanase production using continuous method
Figure 17: Xylanase production using continuous method
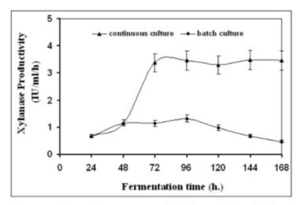 Figure 18: Xylanase productivity comparing batch and continuous method
Figure 18: Xylanase productivity comparing batch and continuous method
This case study shows that although the concentration of xylanase was higher in batch mode, the highest productivity occurred in the continuous method. The productivity increased by almost eight fold, showing that a continuous culture is the best production method (Bakri, 2012).
Mass Transfer for Bioreactors
Mass transfer is important to keep in mind because it often becomes the limiting step of the overall process. The volumetric oxygen transfer coefficient must be known to accurately design and scale up bioreactors. The following equation shows the mass balance for dissolved oxygen in a well-mixed reactor with the absence of biomass:
The variables that affect the values are mostly affected by impeller configuration, speed and aeration. An increase in the gas flow rate makes the values increase (Karimi, 2013).
Types of Bioreactors
- Stirred Tank Fermenter
- The stirred tank fermenter is the most common reactor used for biological reactions (Towler, 2012) and is similar to the stirred tanks discussed previously. It can be used in both batch and continuous mode. Figure 14 shows a stirred tank fermenter.
- Figure 14. Fermentation reactor (Towler and Sinnott, 2013)
- Shaftless Bioreactors
- Shaftless bioreactors are used when the pump shaft seal is considered a non-permissible source of contamination. These reactors use gas flow to provide agitation of the liquid. The design requires careful attention to hydraulics (Towler, 2012). Examples of shaftless bioreactors are shown in Figure 15.
- Figure 15. Examples of shaftless bioreactors (Towler, 2012)
- WAVE Bioreactors
- WAVE bioreactors represent an alternative to standard stainless steel bioreactors. These reactors are flexible and single-use, cutting down time between batches and allow for a more sterile environment. These disposable reactors are mostly used in mammalian cell culture. Three layers of plastic are the minimum necessary for construction. The first is a structural layer, followed by a barrier layer that allows for permeability. The last layer, the fluid contact layer, is designed to take into account inertness and maintain a good seal (Bioprocess, 2013).
- Figure 16. Example of a WAVE bioreactor (GE Health, 2016).
- Packed Bed Bioreactors
- Packed Bed Bioreactors are structured so that the cells are immobilized and placed on large particles. Although they are relatively simple to construct, they can have blockage issues or poor oxygen transfer. There are three types of flow: downward flow, upward flow and the recycling method. In industry, upward flow is preferred, especially when there is gas production during the fermentation (Prieto, 2003).
- Figure 17. Example of a packed bed bioreactor (Kang, 2000).
- Anaerobic Bioreactors
- Anaerobic reactions are used in ethanol production, winemaking, beer brewing, and wastewater treatment. Due to its long standing history, these processes have become well established and improvements include decreasing cost of production due to new technology. Although continuous production for beer has been patented on a large scale, most investment is still focused on batch production (William, 2002).
Preventing Contamination
Since cells are easily affected by both unwanted chemicals and other species in the reactor, bioreactors must be designed in order to avoid contamination (Towler 2013). Bacterial spores are the most demanding sterilization challenge in a bioreactor. Bacterial spores are dormant and non-reproductive structures produced by a small number of bacteria. Since they are meant to ensure survival of bacteria in times of environmental stress, they are heat resistant. In order to ensure that all spores within the medium are killed, the medium must be sterilized (Shuler 2002). There are many methods of sterilization, including filtering, chemical, thermal, and radiation. Thermal sterilization using steam is the most common method, as it is the most economical method for large scale reactors. Chemical agents cannot be toxic to the product, and UV radiation cannot penetrate fluids easily. Steam sterilizations either occur in the fermentation vessel as a batch sterilization or in a continuous apparatus upstream of the fermentation vessel (Seider 2004).
Death Kinetics
- The death kinetics involved in sterilization can usually be described by first order kinetics, but since essentially all contaminants need to be removed, it is usually described in probabilistic terms (Towler 2013). The specific death rate of an organism for thermal inactivation can be described as
- where is the specific death rate, is the Pre-Arrhenius constant, is the activation energy for individual death, and T is the temperature. Sterilization is usually designed for Bacillus stearothermophilus since it is one of the most heat resistant potential contaminants. The death rate for the vitamins in the media must also be considered when designing sterilization, since the nutritional value of the media can be damaged. Short time, high temperature treatment to sterilize media can ensure that the nutritional value is not damaged, but the spores are killed. Typical values for the pre-Arrhenius constant are 1*10^36 and 1*10^4 min^-1 for spores and vitamins respectively. Typical values for the activation energy for individual death are 65 and 10kcal/mol for spores and vitamins respectively (Jewett 2016).
- The number of viable individuals after sterilization can then be described as
- where N is the number of viable individuals, is the number of contaminants initially present, and t is time. The probability of having a contaminated culture can then be described as
- This probability can also be determined with a sterilization chart, using the spore challenge () and , as shown in Fig. 16. The same equations are used for both batch and continuous sterilization, but the spore challenge will be calculated differently, which will be discussed in further sections (Shuler 2002).
- Fig. 18. Sterilization chart (Shuler 2002).
Sterilization of Liquids
Batch
- Batch sterilization is used for smaller fermenters (Biegler 1997). It is usually performed at 121˚C. This is the more widely used technique, since it is a simpler operation than continuous sterilization and no additional materials are added to the media. The disadvantages of batch sterilization are thermal lags and incomplete mixing. Heating requirements are also greater. (DiLeo 2000). The heat up and cool down times from 121˚C to 37˚C are usually longer than the time at the sterilization temperature and can damage the vitamins and protein in the media (Shuelr 2002). The spore challenge for batch sterilization can be calculated with the following equation
- where is the concentration of spores in the media initially and is the total volume of media (Shuler 2002).
Continuous
- The short-exposure and high temperature of continuous sterilization is easier to control, does less damage to the medium, and reduces fermenter downtime. It is also more efficient since it heats small portions of the inlet stream at a time rather than using energy to heat, hold, and cool the entire volume of media at the same time. (DiLeo 2000). The disadvantages, however, are dilution of the medium with steam injection and foaming. (Shuler 2002). A common process for continuous sterilization consists of steam injected into the medium in order to heat it, passing the medium through a holding section to achieve the desired residence time, and then flash cooling the medium. Flash cooling prevents contamination from cooling water (Towler 2013). Diagrams and temperature profiles of batch and continuous sterilization is shown in Fig. 19. The spore challenge for continuous sterilization can be calculated with the following equation
- where is the hold up volume in the reactor, is the residence time, and t is the time spent in continuous mode (Jewett 2016).
- Fig. 19. Diagrams and temperature profiles of batch and continuous sterilization (Shuler 2002).
- Problems involved in sterilization increase greatly with scale-up, as sterilization methods used for lab-bench scale reactions are not acceptable for industry-scale reactions. Given the same medium, a sterilization temperature and time may be enough for a small scale reactor but not for a larger scale. For example, given a of 15 and of 10^4 spores/L, the probability of contamination in a 1L reactor will be 0.003, and in a 10,000 L reactor will be about 1.
- Other considerations
- Since spores will germinate in a moist environment, making them easier to kill as vegetative cells, moist heat is preferred for sterilization. Connections in sterilization equipment must be steam sterilized and trapped air pockets should be avoided. Pipes should be sloped in order to avoid condensate pools and equipment should be pressure tested for leaks. It should be ensured that no viable host cells are in the waste streams and escape to the environment, and exit gas streams also need to be filtered to prevent the escape of microbes to the environment (Jewett 2016).
- If the medium being sterilized contains heat-sensitive materials, filter sterilization must be used instead of steam. Filtration is also used to sterilize the process air used in the system. Microporous filters are used, so the medium must be prefiltered for larger particulates so that the microporous filter does not get clogged. However, filtration is not as reliable as steam sterilization, as any defects in the membrane can lead to contamination, and viruses can often pass through the filter (Shuler 2002).
Example Calculations
A continuous culture is ran in a 1,000L fermentor, and it is desired to have only one in one thousand chance of spore contamination. The fermentation is ran for four weeks at a dilution rate of 0.1hr^-1. The medium initially contains 10^5 spores/L. A sterilization temperature of 140C is used. for the spores is 1*10^36 min^-1, and is 67kcal/mol. There is a key temperature-sensitive vitamin in the broth at a concentration of 10mg/L that has of 1*10^4 min^-1 and of 10 kcal/mol (Jewett 2016).
- To calculate the time needed to sterilize the medium:
- Use the sterilization chart (Fig. 18), with and , to get
- To find k_d,
- Using
- and
- find
- To find the concentration of active vitamin after sterilization,
- First find
- ,
- Then use the equation,
Sterilization of Gases
- Almost all biopharmaceutical production processes involve aeration and therefore require huge volumes of air. For a fermentation lasting five days, up to 200,000,000L of air could be required, and since it is being pumped into the medium, the air must be completely sterile. Air typically has a concentration of microbes of about 1-10 microbes per liter.
- Compressors are required for such large volumes of air, and the adiabatic compression of the air increases the temperature to about 150-220C, and in order to kill spores, the air needs to be at about 220C for about thirty seconds. Therefore, the compression helps to sterilize the air, but since the air cools rapidly as it exits the compressor, and the pipes are hard to maintain as sterile, filtration is necessary to ensure that the entering air is still sterile after it exits the compressor and enters the reactor.
- Filtration of gases is done by either depth or surface filters. In the past, carbon beds with glass wool was used as a depth filter, but if the filter became wet, it would no longer function, as the wet filter provided an easy path for contaminant penetration. The contaminant also needed to come into contact with the glass wool and stick to be stopped. These filters are damaged by steam sterilization, as they show hardening and shrinkage over time. Membrane cartridge filters as surface filters are now more commonly used in industry, as they can get wet and continue to stop contaminants. These filters utilize a sieving effect to remove particles, as membranes have a uniformly small pores that prevent the passage of particles with a larger radius. These filters can also be steam-sterilized without being damaged. Both types of filters increase the pressure drop in the reactor, since the price of energy needed for compressed air for these processes is large, and air treatment can account for a quarter of production costs. However, since high costs are associated with the loss of a batch to contamination, one has to balance the sterility provided from a given filter with minimizing the pressure drop in the reactor (Shuler 2002).
Sterile Sampling
- Sampling the medium in the reactor is necessary to ensure product quality, but it also carries the risk of introducing contamination into the medium. Sampling is usually done about five time a day for a bioreactor. A typical sampling device is shown in Fig. 20. The sampling valve on the reactor is connected to a steam trap to maintain a steam barrier between the reactor and the environment. A sterilized sampling device is attached to the reactor and a valve is attached to the sampling device. Steam runs through the system for about thirty minutes, and then the valves on the reactor and the sampling device are opened to remove the sample (Chisti 1992).
- Figure 20. Diagram of typical sampling device with filter (Chisti 1992).
Cleaning
- Cleaning the fermentation vessel at the end of the production run is necessary in order to remove residual substrates that could lead to contamination of future batches. Cleaning consists of the following wash steps:
- 1. Wash with high-pressure water jets
- 2. Wash with an alkaline cleaning solution, usually 1M NaOH
- 3. Rinse with tap water
- 4. Wash with an acidic cleaning solution, usually 1M nitric or phosphoric acid
- 5. Rinse with tap water
- 6. Rinse with deionized water
- The vessel is drained after each of these steps. For this reason, the vessel should have no internal dead spots where material could accumulate. Also, due to the repeated emptying and filling of the vessel, cleaning leads to significant down time between batches (Towler 2013). A clean-in-place (CIP) system with a transfer flow plate can make cleaning easier, as it connects all the bioreactors and transfer pipes in a plant to one cleaning system, as seen in Figure 21 and 22. The transfer plate has removable pipe sections, providing assurance against mixing of different bioreactor contents (Chisti 1994).
- Figure 21. Example of a clean-in-place system with three bioreactors and a CIP tank (Chisti 1992).
- Figure 22. Delivery of CIP liquids to a bioreactor (Chisti 1994).
Heating and Cooling of Reacting Systems
Exothermic and endothermic reactions will require reactors with heat control systems to prevent operating conditions from falling out of the desired range. Reactor performance is often limited by the ability to add or remove heat. Insufficient heat removal can cause runaway reactions, particularly dangerous situations in chemical processing (Turton et al., 2012). Before considering the design of a heating or cooling system to couple with a reactor, a few important questions should be asked (Towler and Sinnott, 2013).
1. Can the reaction be carried out adiabatically?
2. Can the feeds provide the required heating or cooling? Staged addition of feed can help alleviate the cost of adding a heat exchange network or heat transfer jacket. Also consider adding an inert diluent or hot/cold shots (Seider et al., 2004).
3. Would it be more cost effective to carry out the heat exchange outside of the reactor?
4. Would it be more effective to carry out the reaction inside of a heat transfer device? If a reaction requires only a small volume or small quantities of catalyst, it may be possible to utilize a heat exchanger as a temperature controller and as a reaction location.
5. Does the proposed design allow the process to be started up and shut down smoothly?
6. Are there safety concerns with heating or cooling the reactor?
After considering these aspects of the design, commercial design software such as HYSYS or UniSim can be utilized to estimate heating/cooling requirements. Once this is done, design of the heat exchange system can begin, with different reactor types and reactions requiring different design approaches (Towler and Sinnott, 2013).
Stirred Tank Reactors
Heating and cooling of a stirred tank reactor is done to ensure a uniform reaction temperature, so that there do not exist hot or cold spots within the reactor that can negatively affect selectivity (Towler and Sinnott, 2013).
For indirect heat transfer, there are three main alternatives: a heat transfer jacket, an internal coil, and an external heat transfer circuit. A jacket is utilized as long as there is sufficient heat transfer area for the heat exchange to take place. If this is not the case, coils are used, although the inclusion of a heating coil will significantly increase reactor volume and utility requirements, leading to a large increase in price for the reactor. External circuits contain a heat exchanger that will heat or cool the product stream as required and recycle this material to the reactor to control temperature. External circuits are useful because they can be designed independently of the reactor; sizing the required pumps and heat exchangers will not fundamentally change the activity of the reactor. For any of these choices, it should be ensure that no corrosion of the involved piping will occur, as utility streams bleeding into the reactor can have a very negative impact on the selectivity of the reaction and on the operation of the reactor on a whole (Towler and Sinnott, 2013).
Some direct heat transfer alternatives also exist, as long the reaction in question is compatible with the addition of extra water. Steam can be pumped into the reactor to maintain temperature, which will eliminate the need to design heat transfer surfaces. However, steam injected into the system cannot be recovered, so this will lead to an increase in annual utility costs. Additionally, vapor will be produced if it did not exist previously, so reactors will need to be redesigned to accommodate a vapor removal system (Towler and Sinnott, 2013).
Catalytic Reactors
Slurry Reactors
Since slurry reactors already use a mix of solid catalyst and liquid reactants, any of the methods described in the Stirred Tank Reactors section can be applied to slurry reactors. It is not recommended to use internal coils in such a design, as reactor slurry will often corrode heat exchange material very easily (Towler and Sinnott, 2013).
Fixed-bed Reactors
Indirect heat transfer is not often utilized to control the temperature in fixed-bed reactors, as it hard to maintain uniform temperature across the radial section of the catalyst bed. In cases where temperature control is required, the reactor will be split into smaller sections. After each bed, there will be an heat transfer stage, where the product stream is heated or cooled as necessary and returned to the next catalytic segment (Towler and Sinnott, 2013).
Fluidized-bed Reactors
Fluidized bed reactors have high heat-transfer coefficients, so indirect heat transfer is highly effective. The heat capacity of the solid catalyst particles can be used as a heat transfer medium themselves; heated catalyst contains a reaction location and the necessary heat to maintain the required temperature. Deactivated catalyst is heated during reactivation and recycle (Towler and Sinnott, 2013).
Heat Exchangers as Reactors
It is sometimes necessary to design a reactor as a heat transfer device, like when it is necessary to operate a reactor isothermally and there is a large heat of reaction. Some common situations include high-temperature endothermic reactions that quickly quench without continuous heat input and low-temperature exothermic reactions that must be kept at constant temperature to maintain selectivity. The most common heat transfer equipment used for reactions are shell and tube heat exchangers and fired heaters (Towler and Sinnott, 2013).
Homogenous Reactions
If the reaction does not required a catalyst, than the heat transfer design is the same as a conventional heat transfer device, with some important changes in the thermal design. The usual heat exchanger equations will not apply to the design of a heat exchanger reactor due to the nonlinear behavior of the reaction rate with regards to temperature. In these cases, the usual practice of conservative temperature estimations will not aid in heat transfer design, as greater detail will be required to ensure the proper operation of the reactor. Detailed kinetic models should be developed before designing the internals of the heat transfer device (Towler and Sinnott, 2013).
Heterogenous Reactions
The problems of designing for homogenous reactions still hold for heterogenous ones, with the added complication of solid catalyst beds. Catalyst can be loaded into the tubes of a shell and tube exchanger if the exchanger is mounted vertically and a suitable retaining screen is included at either end of the design. In this instance, hot catalyst can be reliably recycled and heat treated to reactivate the catalysts and reduce the presence of reactor hot spots. High-temperature endothermic reactions will be even more difficult to design for, as their heat requirements often exceed the amount provided by a heated catalyst. In these cases, a "tube in tube" design is utilized, where feed and catalyst are heated simultaneously by an external fired heater. This can be done as long as thermal expansion does not cause damage to the tubes, or else significant catalyst poisoning can occur. The same concerns as detailed in homogenous reactions will still apply for any design utilized for heterogenous ones, so it is again recommended to develop a detailed kinetic model before determining the amount of heat transfer required to maintain proper selectivity (Towler and Sinnott, 2013).
Safety Considerations in Reactor Design
Reactors require much attention to safety details in the design process due to the hazards they impose. They are often the highest temperature point in the process, heat of reaction may be released, and residence times can be long leading to a large inventory of chemicals. Guidelines exist for inherently safer design principles which seek to remove or reduce process hazards, limiting the impact of unforeseen events. These design methods should be applied throughout the design process as part of good engineering practice; they cannot be retroactively added by a process safety specialist. Some examples are given in the table below:
Some Applications of Inherently Safer Design Approaches in Reactor Design (Towler and Sinnott, 2013)
Exothermic reactions require special consideration due to their potential to runaway (temperature rises from heat of reaction being released, increasing reaction rate, releasing more heat, and so on). The reactor must be designed such that temperature can be precisely controlled and the reaction shut down if temperature control is lost. The use of solvents or inert species also allows for temperature control by adjusting heat capacity flow rate relative to rate of heat release from the reaction. An additional safety feature would allow the reactor to be flooded with cold solvent or diluent.
If there is a cooling system it should be designed to return the process to desired temperature if the maximum temperature is reached.
Venting and relief of reactors is complicated by the potential to keep reacting if containment is lost or material is discharged into the pressure relief system. The relief system should be designed according to guidelines outlined in the Design Institute for Emergency Relief Systems (DIERS) methodology. The reactor design team must understand the reaction mechanism and kinetics, including the role of any compounds which may accelerate the reaction. Details may be found on the AIChE website, here.
Capital Cost of Reactors
Reactors are classified as pressure vessels, and as such the pressure vessel design methods can be used to estimate wall thickness and thus determine capital cost. Additional costs come from reactor internals or other equipment. Jacketed stirred-tank reactors require more in depth analysis than that provided by pressure vessel design. The wall of the reaction vessel may be in compression due to the jacket. For preliminary cost estimating a correlation for jacketed stirred tank reactors operating at pressures below 20 bar can be used:
where is the purchased equipment cost on a U.S. Gulf Coast Basis, are cost constants, is the size parameter, and is the exponent for that type of equipment. Values for are given in the table below:
Purchased Equipment Cost Factors (Towler and Sinnott, 2013)
Conclusions
The conversion of feed to products is the essence of a chemical process and, thus, the reactor is the heart of a chemical plant. When designing a reactor, an engineer must first collect data about the chemical reaction and then select appropriate reaction conditions, which will help determine suitable materials of construction. Next, the designer should determine the rate-limiting step and, from this, the critical sizing parameter. Next, preliminary sizing, layout, and costing can be conducted for the reactor. At this point, simulations and experiments can be conducted to verify that the proposed reactor will meet the desired specifications. The design is optimized until these targets are met. Throughout the design process, it is important for the engineer to consider the most appropriate type of reactor to use, any mixing or heat transfer equipment that must be added, and safety considerations.
References
Douglas JM. Conceptual Design of Chemical Processes. New York: McGraw-Hill; 1988.
Seider WD, Seader JD, Lewin DR. Process Design Principles: Synthesis, Analysis, and Evaluation. 3rd ed. New York: Wiley; 2004.
Towler G. Chemical Engineering Design. PowerPoint presentation; 2012.
Towler G, Sinnott R. Chemical Engineering Design: Principles, Practice and Economics of Plant and Process Design. 2nd ed. Boston: Elsevier; 2013.
Turton R, Bailie RC, Whiting WB, Shaewitz JA, Bhattacharyya D. Analysis, Synthesis, and Design of Chemical Processes. 4th ed. Upper Saddle River: Prentice-Hall; 2012.
Westfall, Patrick J., and Timothy S. Gardner. "Industrial fermentation of renewable diesel fuels." Current opinion in biotechnology 22.3 (2011): 344-350.
Schmidt, F. R. "Optimization and scale up of industrial fermentation processes." Applied microbiology and biotechnology 68.4 (2005): 425-435.
Yurimoto, Hiroya, et al. "Regulation and evaluation of five methanol-inducible promoters in the methylotrophic yeast Candida boidinii." Biochimica et Biophysica Acta (BBA)-Gene Structure and Expression 1493.1 (2000): 56-63.
Huang, Hua-Jiang, et al. "A review of separation technologies in current and future biorefineries." Separation and Purification Technology 62.1 (2008): 1-21.
Stephanopoulos, George, Aristos A. Aristidou, and Jens Nielsen. Metabolic engineering: principles and methodologies. Academic press, 1998.
Nothaft, Harald, and Christine M. Szymanski. "Protein glycosylation in bacteria: sweeter than ever." Nature Reviews Microbiology 8.11 (2010): 765-778.
Shuler, ML, Kargi, F. Bioprocess Engineering Basic Concepts. 2nd ed. Upper Saddle River: Prentice-Hall. 2002: 315-320
L.T. Biegler, I.E. Grossmann, A.W. Westerberg, Systematic Methods of Chemical ProcessDesign, Prentice-Hall: Upper Saddle River, 1997.
Shuler, Michael L., and Fikret Kargi. Bioprocess engineering. New York: Prentice Hall, 2002.
Arsenault, Patrick R., Kristin K. Wobbe, and Pamela J. Weathers. "Recent advances in artemisinin production through heterologous expression." Current medicinal chemistry 15.27 (2008): 2886.
Karimi, Ali, Golbabei, Farideh, Pourmand, Mohammad. “Oxygen mass transfer in a stirred tank bioreactor using different impeller configurations for environmental purposes.” Iranian Journal of Environmental Health, Science, and Engineering, 2013.
“WAVE Bioreactor 500/1000 System.” Bioprocess Online, 2013.
“WAVE Bioreactors.” GE Healthcare Life Sciences, 2016.
Prieto, G., Okumoto, M., Gay, C.R. “Nonthermal plasma reactors for the production of light hydrocarbon olefins from heavy oil.” Brazilian Journal of Chemical Engineeirng, 2003.
Kang, Xuezhen. “Packed Bed Bioreactor.” 2000.
Y. Chisti, Assure Bioreactor Sterility, Chemical Engineering Process. 1992: 88(9): 80-85.
M. Jewett. Media Design. ChBE 375: Biochemical Engineering Class Notes. January 12, 2016.
Y. Chisti, M. Moo-Young. Clean-in-place systems for industrial bioreactors: design, validation and operation. Journal of Industrial Microbiology. 1994: 13: 201-207.
G. DiLeo and S. Ogoreuc. “Sterilization”. Rensselaer Polytechnic Institute. 2000. http://www.rpi.edu/dept/chem-eng/Biotech-Environ/Projects00/sterilize/sterilization.html. Accessed February 20, 2016.
Y. Bakri, Y. Akeed, P. Thonart. "Comparison between continuous and batch processing to produce xylanase by penicillium canescens 10-10c." Brazilian Journal of Chemical Engineering, 2012.



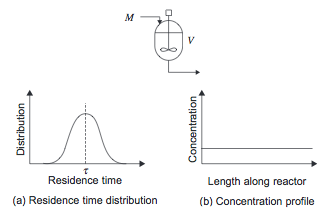
![{\displaystyle \Delta H_{\text{r,P,T}}=\Delta H_{\text{r}}^{\circ }+\int _{1}^{P}\left[\left({\frac {\partial H_{prod.}}{\partial P}}\right)_{T}-\left({\frac {\partial H_{react.}}{\partial P}}\right)_{T}\right]dP+\int _{298}^{T}\left[\left({\frac {\partial H_{prod.}}{\partial T}}\right)_{P}-\left({\frac {\partial H_{react.}}{\partial T}}\right)_{P}\right]dT}](https://wikimedia.org/api/rest_v1/media/math/render/svg/268310edb96f906d4e87282cd3da371a0e05c15b)




















![{\displaystyle D_{v}={\frac {1.013\times 10^{-7}T^{1.75}{\left({\frac {1}{M_{a}}}+{\frac {1}{M_{b}}}\right)}^{1/2}}{P{\left[{\left(\sum _{a}v_{i}\right)}^{1/3}+{\left(\sum _{b}v_{i}\right)}^{1/3}\right]}^{2}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c9be45b7d1a85b5a6d4d71a69116e3e0bd7dbbc1)