Equipment sizing
Author: Matt Nathal [2015] Lauren Burke [2016]
Stewards: Jian Gong and Fengqi You
Vessel Specifications

The process requirements usually dictate specifications and parameters that the pressure vessel must fulfill. Some such requirements are:
- Minimum and Maximum design temperature
- Minimum and Maximum design pressure
Design Temperature
Determining a maximum and minimum design temperature for a pressure vessel is important because the strength of metals decreases as temperature increases. Using a temperature margin to account for all possible uncertainties in the process helps ensure safety and stays within ASME codes. [2]
Common margins used for pressure vessel design temperatures are as follows:
Maximum design temperature – highest mean metal temperature expected in operation plus a margin (typically 50°F).
Minimum design temperature – lowest mean metal temperature expected in operation minus a margin (typically 25°F).
Steps should be taken to account for potential failures of cooling/heating streams to prevent or minimize damage to equipment and injury to operators.[2]
Design Pressure
Normal operating pressure – the expected pressure of the process.
Maximum operating pressure – the highest expected pressure, potentially during startup, shutdown, or emergencies.
Design pressure – the maximum operating pressure plus a margin. The margin is typically the greater of: 10% of max operating pressure or 25 psi.
The specified pressure is usually near the relief valve at the top of the vessel.
Vessels under external pressure (jacketed or those under vacuum) need to be able to resist the maximum differential pressure that can occur in the process. Often, vessels under external pressure are also fitted with internal stiffening rings as suggested by the BPV code. Additionally, it is recommended that vessels under vacuum be designed at a pressure of -1 bar unless fitted with an effective vacuum breaker.[2]
Vessel Geometry
Pressure Vessel Size and Shape
Typically pressure vessels are cylinders with at least a 2:1 ratio of height to width. 3:1 and 4:1 ratios are most common.[2]
Pressure Vessel Orientation
Pressure vessels can be oriented either vertically or horizontally. Vertical vessels are more common because they use less land space and the smaller cross-sectional area of the vessel allows for easier mixing. Horizontal vessels are used when more phase separation is required because larger cross-sectional areas allow for less vertical velocities and therefore less entrainment. Settling tanks and flash vessels are typically horizontal for this reason. Horizontal vessels also allow easier cleaning, so heat exchangers are primarily horizontal.[2]
Head Design
There are three different designs for the ends of the pressure vessel: hemispherical, ellipsoidal, and torispherical.
Hemispherical heads are best for high pressure systems, they provide the largest internal volume of the three options, they are half the thickness of the shell, and are the most expensive to make and combine with the shell.
Ellipsoidal heads are cheaper than hemispherical heads and provide less internal volume, they are the same thickness as the shell, and are most common for systems with greater than 15 bar.
Torispherical heads are the cheapest of the three options, and are most commonly used when pressures do not exceed 15 bar. The two junctions in a torispherical end closure are between the head and the cylinder, and at the junction of the crown and knuckle radii. Bending and shear stresses can occur at these points and needs to be accounted for. The crown radius should not be larger than the diameter of the cylinder section, and the ratio of the knuckle to the crown radii should not be less than 0.06. [2]
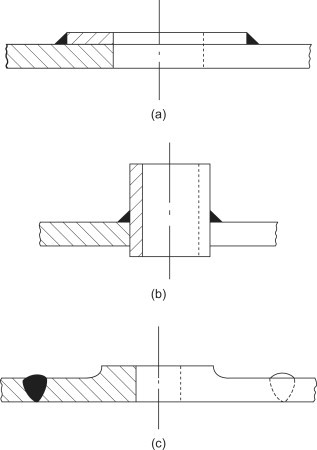
Compensation for Openings and Branches
Openings and branches in pressure vessels are used to connections, manways, and instrument fittings. Having an opening inherently weakens the shell, making stress concentrations likely. In order to compensate for this, wall thickness is increased in the area around of an opening. It is necessary to provide support without changing the existing dilation pattern around the opening of the vessel. If the wall is over-reinforced, it can cause a “hard spot” which makes the wall less flexible and can cause additional secondary stresses. To calculate the minimum amount of reinforcement needed for an opening or branch, use ASMA BPV Code Sec. VIII D.1 Part UG-37.
The most common method to reinforce openings is by welding a collar or pad around the opening, typically with an outer diameter about 1.5 to 2 times the opening’s diameter (Figure 2(a)). This method, while common, does not provide the best support around the opening because thermal stresses can arise due to poor thermal conductivity at the junction of the shell and the pad.
Branches are commonly reinforced by allowing the branch to protrude into the vessel (Figure 2(b)). It is important to use caution with this method, as the protruding branch can trap particulates and corrosion can occur in the created crevices.
Enforcing rings (Figure 2(c)) are the most expensive method of reinforcement, but are also the most expensive. Because of this, they are typically only used for large openings in vessels under severe operating conditions.[2]
Stresses and Strains
There are a variety of potential stresses on a pressure vessel that must be accounted for during design and construction:[2]
- Internal and external pressure
- Weight of vessel
- Weight of contents
- Weight of internals (distillation trays, heating/cooling coils, packing supports)
- Weight of attached equipment
- Thermal expansion
- Cyclic loads caused by condition changes
- Friction loads
- Environmental loads (wind/snow/seismic)
Wall Thickness
There are two main stresses that can occur on the shell portion of the pressure vessel; hoop stress and longitudinal stress.
Hoop Stress:
Wall thickness
Longitudinal Stress:
Wall thickness
Where P is the pressure, D is the diameter, S is the max allowable stress, and E is the welded joint efficiency. The thicker of the two is chosen as the wall thickness. The minimum wall thickness (without considering corrosion allowances) is 1/16 inches.
Typically walls are much thicker. In high pressure vessels, internal pressure has the largest magnitude. In low pressure vessels, wall thickness is designed to resist vacuum.[2]
Head thickness
Alternate equations govern the appropriate head thickness:
Hemispherical:
Thickness
Ellipsoidal:
Thickness
Torispherical:
Thickness
Rc is the crown radius.[2]
Corrosion Allowance
A margin of wall thickness must be added to account for corrosion of the vessel over time. This margin is usually between 1/16” and 3/16”.
In heat exchangers where wall thickness can affect heat transfer, smaller margins are used.[2]
Case Studies
Determine Wall Thickness
What is the wall thickness of a 304 stainless steel pressure vessel with a 5ft diameter, 400 psi design pressure, and 500F design temperature? Assume double-welded butt joints were used (E = 0.85).
First, the max allowable stress must be calculated. Using a table found in: ASME BPV Code Sec. VIII D.1, Sec. II Part D[4], the maximum allowable stress under these conditions is 12,900 psi. The hoop stress is calculated as follows:
The longitudinal stress is then calculated:
The larger of the two is hoop stress. Adding on the corrosion allowance and rounding to the nearest quarter inch gives a wall thickness of 1.25 inches.
Nozzle Design
Find the wall thickness required for the following nozzle.[5]
Given:
Interior Pressure (P) of 201.4 psi
Allowable stress (S) of 17100 psi
Assume a nozzle efficiency (E) of 1 and a nozzle corrosion allowance (nca) of 0.01 inches
Undertolerance Allowance (UTP) of 12.5%
Need to determine R for the nozzle
Here, can use the same equations used for determining stresses in pressure vessel heads.
check if Nwall is enough?
Wall thickness is large enough
References
- ^ "ASME Pressure Vessels". EnviroSep. http://envirose.s436.sureserver.com/APVCS/asme-pressure-vessels.html. Accessed 2/28/15
- ^ a b c d e f g h i j k l Sinnott, R. K., and Gavin P. Towler. Chemical Engineering Design / Ray Sinnott, Gavin Towler. 2013
- ^ "Pressure Vessel Heads". Inspection-for-Industry. http://www.inspection-for-industry.com/pressure-vessel-heads.html. Accessed 2/5/15
- ^ ASME. Boiler and PRessure Vessel Code: An International Code. http://www.asme.org/wwwasmeorg/media/ResourceFiles/Shop/Standards/New%20Releases/ASME-BPVC-Brochure.pdf 2015
- ^ "Sample Vessel Calculations" Pressure Vessel Engineering Ltd. http://www.pveng.com/ASME/DesignTools/ASME9_FEA_Report.pdf Accessed 2/21/2016
![Seen above: (a) ellipsoidal, (b) torisphereical, and (c) hemispherical.[3]](/images/f/f2/Pressure_vessel_heads.jpg)