Pinch analysis

Author: Micah Zuckerman ^[2015]

Stewards: Jian Gong and Fengqi You

Introduction

Pinch analysis is a methodology used to minimize energy consumption of chemical processes by optimizing energy recovery methods. A pinch occurs at the closest point of approach between hot and cold streams in the network. By designing around this point energy from utilities can be minimized. This page focuses on pinch analysis in the context of heat exchanger networks (HENs), however similar methods can be used in the design of mass exchanger networks (MENs).

Pinch technology

For maximum energy recovery (MER), energy should not be transferred across the pinch. The network is separated into hot and cold regions, above and below the pinch respectively. In the hot region, streams are matched so that heat is transferred from the coolest possible source. Below the pinch, the opposite occurs. This yields the minimum utility requirement solution to the heat exchanger network. Minimum utility requirement is not necessarily the optimum solution, however, the solution with the lowest overall cost is. Minimizing the size and quantity of heat exchangers plays a large role in decreasing capital costs. There is a trade-off between operational and capital costs. In some cases transfer across the pinch is necessary to produce the optimal network. For more information see the trade-off section of the Sensitivity analysis and design optimization page.

Minimum approach temperature

The minimum approach temperature represents the smallest gap in temperature across which heat transfer will occur in the system. This often only occurs at the pinch. While technically any value greater than zero can allow for heat transfer, very small values are not often feasible. Low temperature differences decrease the need for additional utilities, but require increasingly large heat transfer areas, meaning larger heat exchangers. The trade-off between operating costs and capital costs should be used to choose the minimum approach temperature for the network. Typical choices for minimum approach temperatures are between 5 °C and 30 °C (Towler and Sinnott 2013).

Analysis Methods

Pinch technology is a highly used and advanced technology throughout industry. Because of this, there have been devised multiple approaches with which to solve a pinch system.

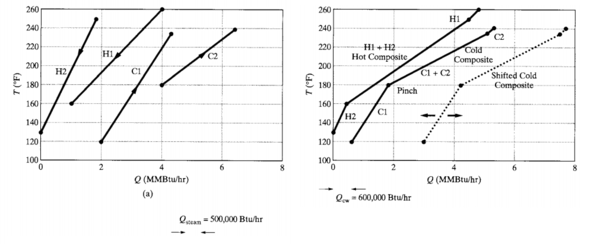
Composite curves method

Example of composite curve method taken from Sieder et al. Fig 10.7

This method uses a graphical approach and makes obvious the presence and location of the pinch in the system. First one combines all hot streams into single composite curve on a temperature-enthalpy graph. The same is then done with the cold streams. Plotting both composite curves on a temperature-enthalpy plot reveals a pinch at the point where the cold and hot curves are closest in temperature. Because change in enthalpy is the feature of concern, the composite curves can be freely shifted along the enthalpy axis. In this manner the minimum approach temperature can be satisfied at the pinch.

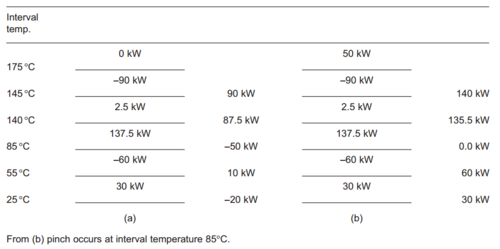
Problem table method

The problem table method, also known as the cascade method, forgoes graphs for a numerical approach. This method is useful when solving heat-exchanger network problems manually, but has fallen into disuse due to the advent of modern computing. The first step in the process is converting stream temperatures into interval temperatures. To do this, one subtracts half the minimum approach temperature from the hot stream temperatures, and adds half to the cold stream temperatures. The intervals are then ranked in order of magnitude, ignoring any repetitions. The next step involves balancing the heat carried by streams between each interval. Any excess heat cascades over into the next lower down interval. Add heat from the top of the system eliminate any negative values. The amount added at the top corresponds to hot utility duty, while the remaining value at the bottom corresponds to heat that must be removed by cold utility.

Example of the problem table method. The right most column contains both the minimum heating requirement for the system at the top, and the minimum cooling requirement at the bottom

Computer tools for HEN design

Presently, the two previously described methods of pinch analysis are not in wide use in industry; rather analysis is performed by specialized software. These software include: Aspen HX-Net™ from Aspen Technology Inc., SUPERTARGET™ from Linnhoff March Ltd. and UniSim™ ExchangerNet™ from Honeywell International Inc. (Towler and Sinnott 2013). Stream data is often pulled directly from the process simulations by the software package. Automatically generated networks must be properly constrained lest an unfeasible amount of stream splits and loops be generated. There is great value, however, in the ability of software packages to perform many tweaks and iterations to fine tune a network.

Example problem

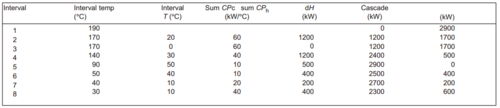
In this example problem we will use pinch analysis via the problem table method to design a heat exchanger network given the following stream table, taken from Towler and Sinnott, and a desired minimum approach temperature of 20°C.

Stream	Number Type	Heat Capacity Flow Rate, kW/°C	Source Temp. °C	Target Temp. °C	Heat Load, kW
1	hot	40.0	180	40	5600
2	hot	30.0	150	60	1800
3	cold	60.0	30	180	9000
4	cold	20.0	80	160	1600

The first step is to calculate the interval temperatures. Because the minimum approach temperature is 20°C, the interval temperatures for the hot stream are 10 °C less than the actual temperature and those for the cold stream are 10°C more than the actual temperature. The next step is to rank the interval temperatures, ignoring any duplicated values. We then determine what streams belong in which interval. The sum of CP values for the cold streams minus that for the hot streams can then be multiplied by the interval ΔT to give the interval ΔH, and the interval ΔH values can be cascaded to give the overall heat flow.

Problem table exhibiting cascade taken from Figure 3.28 of Towler and Sinnott

The amount of heat added at the top to remove any negative values, 2900 kW, is the hot utility. The 600 kW left over at the bottom is the cold utility required. The pinch occurs where the heat transferred is zero, that is at interval number 4, interval temperature 90 °C. This is equivalent to 100°C in the hot stream or 80°C in the cold stream.

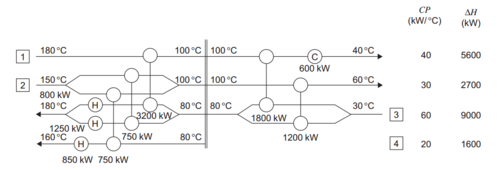
Now we need to design the actual system:

Above Pinch

1. CPh ≤ CPc
2. It is possible to match stream 1 or 2 with stream 3 but neither stream can match with stream 4. This is problematic, since if we match stream 1 with 3 then stream 2 will not be able to make a match at the pinch. Likewise, if we match stream 2 with 3 then stream 1 will not have a match at the pinch.
3. Check the heat available in bringing the hot streams to the pinch temperature.

   stream 1 ΔH = 40.0(180 − 100 )= 3200 kW

   stream 2 ΔH = 30.0 (150 − 100 ) = 1500 kW

4. Check the heat required to bring the cold streams from the pinch temperature to their target temperatures.

   stream 3 ΔH = 60.0(180 – 80)= 6000 kW

   stream 4 ΔH = 20.0(160 – 80) = 1600 kW

5. If we split stream 3 into two branches with CP of 40.0 and 20.0, then we can match the larger branch with stream 1 and transfer 3200 kW, which satisfies (ticks off) stream 1.
6. We now have two cold streams, both with CP of 20.0, and one hot stream (2) with CP of 30.0. We need to split stream 2 into two branches. As an initial guess these can both have CP of 15.0. We can then match one branch of stream 2 with the smaller branch of 4 and transfer 750 kW, and the other branch with stream 3, also for 750 kW, which then ticks off stream 2.
7. Include a heater on the larger branch of stream 3 to bring it to its target temperature:

   ΔHhot = 40 (100 ) − 3200 = 800 kW

8. Include a heater on the smaller branch of stream 3 to provide the balance of the heat required:

   ΔHhot = 20 (100 ) – 750 = 1250 kW

9. Include a heater on stream 4 to provide the balance of the heat required:

   Δ Hhot = 1600 − 750 = 850 kW

10. Check sum of heater duties = 800 + 1250 + 850 = 2900 kW = hot utility target.

Below Pinch

1. CPh ≥ CPc
2. Note that stream 4 starts at the pinch temperature and so cannot provide any cooling below the pinch.
3. We cannot match stream 1 or 2 with stream 3 at the pinch.
4. Split stream 3 to reduce CP. An even split will allow both streams 1 and 2 to be matched with the split streams adjacent to the pinch, so try this initially.
5. Check the heat available from bringing the hot streams from the pinch temperature to their target temperatures:

   stream 1 ΔH = 40.0 (100 − 40 ) = 2400 kW

   stream 2 ΔH = 30.0 (100 − 60 ) = 1200 kW

6. Check the heat required to bring the cold streams from their source temperatures to the pinch temperature:

   stream 3 ΔH = 60.0 (80 − 30 ) = 3000 kW

   Stream 4 is at the pinch temperature

7. Note that stream 1 cannot be brought to its target temperature of 40 °C by full interchange with stream 3 as the source temperature of stream 3 is 30 °C, so ΔTmin would be violated. So transfer 1800 kW to one leg of the split stream 3.
8. Check temperature at exit of this exchanger:

   Temp out= 100 – 1800/40= 55 °C, satisfactory

9. Provide cooler on stream 1 to bring it to its target temperature; the cooling needed is

   ΔHcold = 2400 − 1800 = 600 kW

10. Transfer the full heat load from stream 2 to second leg of stream 3; this satisfies both streams.

Proposed Heat Exchanger Network for example problem from Figure 3.29 of Towler and Sinnott

References

Biegler LT, Grossmann IE, Westerberg AW. Systematic Methods of Chemical Process Design. Upper Saddle River: Prentice Hall; 1997.

Seider WD, Seader JD, Lewin DR. Process Design Principles: Synthesis, Analysis, and Evaluation. 3rd ed. New York: Wiley; 2004.

Towler G, Sinnott R. Chemical Engineering Design: Principles, Practice and Economics of Plant and Process Design. 2nd ed. Boston: Elsevier; 2013.

Turton R, Bailie RC, Whiting WB, Shaewitz JA, Bhattacharyya D. Analysis, Synthesis, and Design of Chemical Processes. 4th ed. Upper Saddle River: Prentice-Hall; 2012.