Property package
Authors: Yuanxi Zhao [2016]
Steward: Daniel Garcia, Fengqi You
Introduction
Students and young chemical engineers often find themselves relying on powerful process simulation programs for coursework or job performance without having the proper background in applied phase equilibrium thermodynamics. This lack of experience becomes obvious when either a poor choice is made in selecting a physical property package or the actual selection process is completely overlooked. Property package is aspects of equations used for the determination of physical properties of the components to simulate. It is also named the thermodynamic model. The selection of a suitable thermodynamic property package to predict the vapor-liquid equilibrium for the studied component is important, as it can affect the simulation results considerably.
Background
Proper selection of thermodynamic models during process simulation is absolutely necessary as a starting point for accurate process simulation. A process that is otherwise fully optimized in terms of equipment selection, configuration, and operation can be rendered essentially worthless if the process simulation is based on inaccurate thermodynamic models. Because of this, good heuristics and appropriate priority should be placed on both selecting thermodynamic models and reporting the selections in process reports.
During process simulation, thermodynamic property package selection should be performed in at least two steps. Firstly, as with initial process configurations, the thermodynamic model should be chosen based on heuristics (heuristics) that provide for a good base case but may or may not provide the desired level of accuracy. Secondly, based on the results of the base case simulation (complete with cost estimate), improving the accuracy of the thermodynamic property package should be prioritized relative to optimizing other design parameters such as the configuration of unit operations, optimization of specific unit operations, heat integration, and other degrees of freedom used to optimize processes. Optimization includes both economic and simulation accuracy aspects. Thermodynamic property package definition should be revisited as often as necessary during process optimization.
Selection of the Property Model
Decision Trees
To perform an adequate selection, the various parameters of the components to take into account are proposed. With the objective of performing an adequate and responsible selection, many articles and books have been published. The more recognized medical is the one developed by the Aspen technology symbol engineer, Eric Carlson, who summarizes some main parameters for the selection in several decision trees that are shown as the following reference.
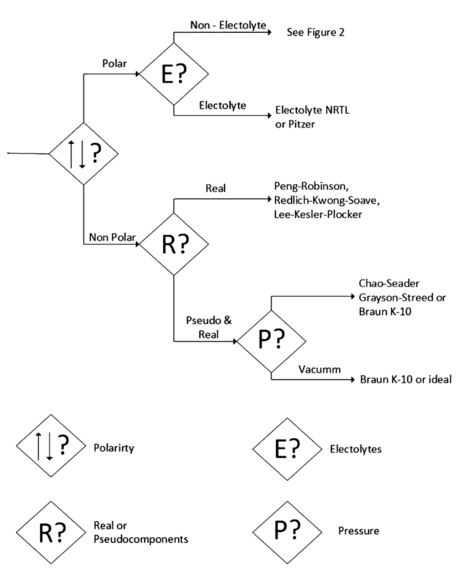
In Figure 1 the first criteria to take into account for the selection of the thermodynamic models are indicated. The polarity is an important aspect because it determines the type of molecular interaction that can take place between the substances. It can be deducted that if the polarity is high, the interaction is strong. The second parameter taken into account depends on the first one; it means, that the mixture or at least one of the component is polar it has to be considered as the substance is not an electrolyte. This parameter is relevant because the electrolytic mixtures are composed of ions obtained from salts. The application of these type of mixtures include Ash wash, neutralization, acid production and salt precipitation.
For non-polar substances, the existence of pseudo-components has to be considered. These are employed in very complex nonpolar mixtures, as is the case of petroleum, in which, since some components cannot be identified, and representation of a set of components is generated, generally classified by similar properties, like boiling point, to reduce the number of them.
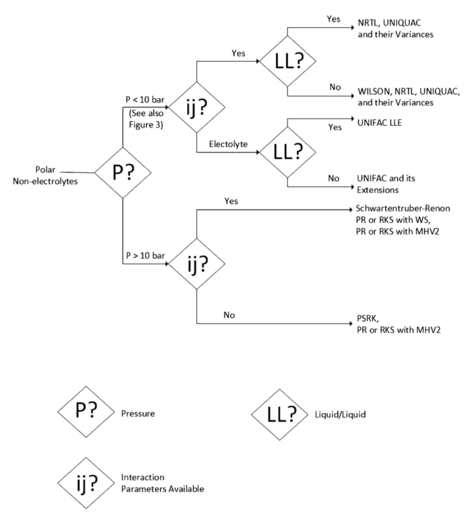
The properties of these pseudo-components are obtained like the average of the component's properties. In Figure 2 subsequent decision tree for a polar mixture of non-electrolytes is present.
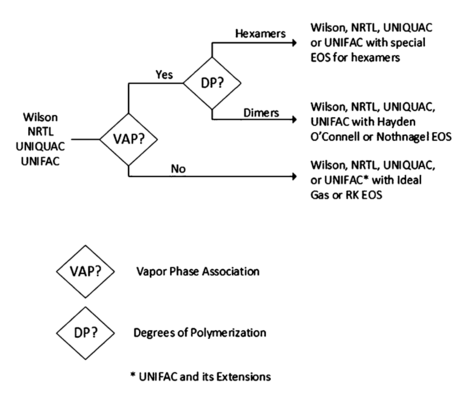
In Figure 3, a decision tree adequate for parameters related with the presence of polymers in the simulation is present.
Five main tasks
In general, there are five main tasks for the proper representation of the physical properties:
- Select and adequate physical property method
- Validate the physical properties
- Properly describe the components that are not present in the database and the missing parameters
- Obtain and use experimental data
- Estimate any missing parameter
This process may not be sequential and can be concurrent sometime. Additionally, to the correct selection of the model, it has to be correctly implemented, because there are situation,s like in the case of partial molar properties that the model does not contemplate and that may be of the importance for the modeling of an operation of process.
Modeling Phase equilibrium
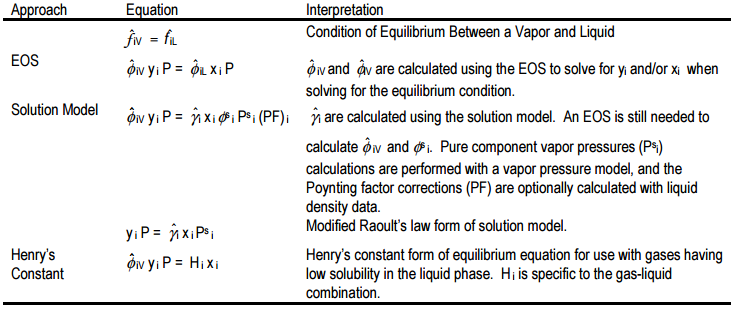
Thermodynamic property package selection is, appropriately, one of the first necessary steps in process simulation. These packages typically include EOSs, activity (solution) models and other more specialized models for the purpose of taking account non-idealities in vapor and liquid mixtures. Table 1 summarizes the parameters that are calculated in these approaches. Vapor pressure models (e.g. Extended Antoine equation) are generally accurate provided the parameters are not specific to a range outside that of interest. Corresponding states methods for pure component fugacity coefficients (e.g. Chao Seader Model) are typically only called upon for pure component calculations when alternatives are not available. Selection of either vapor pressure models, pure component fugacity models, or other methods such as interpolation of available data are typically performed automatically by simulation packages only as necessary and without operator interaction.
Vapor Liquid Equilibrium Model Selection
As summarized by the EOS and solution model equations of Table 1, both an EOS and solution models can be used for VLE calculations. Due to the complexity of the EOS calculations, this approach to the solution of mixture VLE problems is typically not covered in undergraduate curriculum. Walas provides good examples and algorithms for these calculations. The following heuristics provide a good approach to base case calculations:
- When the highest reduced temperature for VLE processes as calculated by Kay’s rule is greater than 0.75 and immiscible liquid phases are not anticipated, use an EOS for VLE calculations. For Kay’s rule, Tr = T / ΣyiTci. The EOS selection will typically be limited to cubic equations capable of VLE modeling such as the Peng Robinson (PR) or Soave Redlich Kwong (SRK) EOSs.
- When selecting an EOS, EOSs that have binary interaction coefficients obtained from experimental data should be selected over EOSs in which these are not available. Check the simulator’s listing of these binary interaction coefficients through options that are typically provided by the simulator after an EOS is selected.
- When the reduced temperature as calculated by Kay’s rule is less than 0.75, use a solution model for the liquid phase and an EOS for the vapor phase.
- The better-known solution models include equations Margules, van Laar, Wilson, NRTL, and UNIQUAC models. Of these, based on frequencies of best fits, the following choices are best when only one liquid is anticipated:
- a) for aqueous organics, NRTL
- b) for alcohols, Wilson
- c) for alcohols and phenols, Wilson
- d) for alcohols, ketones, and ethers Wilson or Margules (Wilson is preferred due to its improved ability to correct for changes in temperature)
- e) for C4-C18 hydrocarbons, Wilson
- f) for aromatics Wilson or Margules (Wilson is preferred due to its improved ability to correct for changes in temperature)
- g) When in doubt for VLE calculations, use the Wilson equation. Apply this rule under the assumption that binary interaction coefficients are available or can be estimated.
- When performing simulation that involves LLE, do not use the Wilson equation since the Wilson equation is not capable of performing LLE calculations. Alternative to the Wilson equation use the TK Wilson equation or the NRTL equation. Apply this rule under the assumption that binary interaction coefficients are available or can be estimated.
- If your simulation package does not provide the ability to estimate binary interaction coefficients with the Wilson, NRTL, or TK Wilson equations and does offer this ability with the UNIQUAC equation, then use the UNIQUAC solution model with UNIFAC estimation of binary interaction parameters.
- If the critical properties of a component are not available, the use of a cubic equation may not be an option. If within this same simulation, some process conditions have a reduced temperature at VLE conditions greater than 0.75, several approaches are available.
- a) the use of solution models may be extended with increasing inaccuracy to reduced temperatures of about 0.9,
- b) the process may be separated into different sub-processes that can be modeled using different thermodynamic packages,
- c) the process may be modified for simulation purposes only to allow it to be divided into sub-processes that can be modeled using different thermodynamic packages, and
- d) the critical properties may be estimated for those components for which critical properties are not available.
If critical properties are not available for certain components and it is anticipated that processes will have VLE processes near the component critical point, this should indicate a potential problem to the engineer. For example, in the case of ethylene oxide, critical properties are not available because it explodes prior to experiencing its critical point. In the case of oleic acid, the acid simply degrades prior to reaching its critical point. In both of these cases, it would be impractical to design a process to operate with these components at VLE near their critical points.
The use of reduced temperature for selecting EOS models over solution models is based on two premises. Since solutions models are specifically designed for liquid phases and are fitted to data in the conventional liquid phase as compared to near-critical fluids, solution models will tend to be more accurate than EOSs for liquids. With increasing temperatures and at a reduced temperature of about 0.75, the liquid phase begins to expand rapidly to the point where polar and hydrogen bonding forces that dominate liquid phase properties become less dominating. Since these polar and hydrogen bonding forces largely determine the binary interaction coefficients, the binary interaction coefficients become increasing invalid and the model becomes increasingly inaccurate. EOSs are specifically designed to be useful in these near-critical regions, and so, they are preferred. The best reduced temperature to use as a point of transition is dependent upon the engineer, but the use of values from 0.7 to 0.8 can be readily justified by studying compressibility charts.
The choice of which EOS is substantially personal preference provided the EOS is capable of performing the desired tasks—this typically translates to limiting the selection to cubic equations if an EOS is used to model both liquid and gas phases. When teaching design for the first time at The University of Kansas, I asked Professor Walas which equation of state was generally the best, he responded that whenever somebody develops and reports a new EOS, they claim it to be better than the previous EOS options. The SRK EOS appears to be the most favorite with the PR EOS a close second. Walas reports binary coefficients for several systems and most simulation packages have these or other binary interaction coefficients built into their databases.
Table 2 summarizes a comparison of solution models presented by Walas. These data were used to derive heuristic 4. Heuristic 4 is also based on the ability of the model to go beyond fitting data, and specifically, to the ability of the solution model to accurately account for the impact of temperature. Based on the ability to accurately account for changes in temperature, the Wilson equation was selected over the Margules equation even though the Margules equation may provide a slightly better fit to the data.
| Mixture Classification | Wilson | NRTL | UNIQUAC | Best Fit |
|---|---|---|---|---|
| Aqueous organics | 0.240 | 0.403 | 0.143 | NRTL |
| Alcohols | 0.395 | 0.223 | 0.131 | Wilson |
| Alcohols and phenols | 0.342 | 0.225 | 0.102 | Wilson |
| Alcohols, ketones, ethers | 0.243 | 0.155 | 0.155 | Wilson |
| C4-C6 hydrocarbons | 0.365 | 0.232 | 0.099 | Wilson |
| C7-C18 hydrocarbons | 0.260 | 0.209 | 0.136 | Wilson |
| Aromatics | 0.225 | 0.160 | 0.172 | Wilson |
The heuristics described above are designed to provide a starting point for selection of thermodynamic packages to use for base case process simulation. Depending upon process and availability of data, the best choices of thermodynamic packages will vary.
It is interesting to note that even though the development of the UNIQUAC solution model in combination with the UNIFAC group contribution was groundbreaking work, the UNIQUAC model does not consistently fit experimental data well. When using UNIFAC or other group contribution methods, different binary coefficients will be estimated based on LLE versus VLE options. The applicable options or options should be chosen during process simulation.
Selection of Model for Gas Solubility in Liquids
The equilibrium of a gas with a liquid can and should be separated into two separate types of separation problems:
- the separation of a volatile organic from a gas like nitrogen
- the separation of the gas from a liquid
The separation of volatile organic compounds from purge gases is commonly encountered in industry. For this system, the gas is typically sparingly soluble in the liquid, and because of this, solution models such as the Wilson equation accurately estimate the vapor pressure of the volatile organics. In contrast, accurate modeling of a sparingly soluble gas in a liquid is typically only achieved if experimental values are available to specify binary interaction coefficients at the low concentrations of the gas. The solubility of a gas can vary considerably depending upon the liquid. Furthermore, when comparing estimates of the SRK EOS to the Wilson equation, the estimated solubility can easily vary by greater than an order of magnitude. This second type of gas-liquid solubility problem requires further discussion to develop successful strategies.
By far, the best resolution of uncertainty issues related to the solubility of gases in liquids is to do a sensitivity study. This could be a formal simulation sensitivity study or a thought process. In many instances, equipment sizes and configurations as well as bottom-line economics are substantially not impacted even if gas solubility in a liquid is varied by two orders of magnitude. In such instances, even if the thermodynamic model is off by a factor of 10, the soundness of the design is not impacted. When the gas solubility does impact equipment design or economics data should be pursued.
Examples of Equations of state used in property package
The equations of state are models that correspond to PVT correlations that allow to estimate the properties of a pure substance or of a mixture using the Maxwell Relations; in the case of mixtures, mixing rules design for that purpose are employed.
The most important equations of state are the cubic equations, since they combine mathematical simplicity with a good approximation of the theoretical values of the estimated properties. Some of the most widely used equations of state are:
Redlich-Kwong Equation
Introduced in 1949, the Redlich-Kwong (RK) equation was a substantial improvement with respect to other equation of its time. It is still focus of attention due to its relative simple expression.
Although it is better than the Van der Waals equation, it does not provide good results for the liquid phase, and therefore it cannot be used for vapor liquid Thermodynamic and Property Models equilibrium calculations. Nonetheless, in such cases it can be employed jointly with concrete expressions for the liquid phase.
The Redlich-Kwong equation is adequate to determine vapor phase properties when the ratio of the pressure and the critical pressure is lower than half the ratio of the temperature and the critical temperature.
The corresponding model is presented as follows:
where:
molar volume
Soave-Redlich-Kwong
In 1972, Soave replaced the term of of the Redlich-Kwong equation with the expression , function of the temperature, and the acentric factor. The _ function was conceived to fit with the vapor pressure data of hydrocarbons; this equation describes accurately the behavior of those substances. It can be used to correctly represent both liquid and vapor phases.
The model with the corresponding correction is shown below:
The advantage of using this model in a simulation package are
- It is a modification of the Redlich-Kwong model
- Results similar to the Peng-Robinson (PR) model but with a lower development than in Aspen Hysys can be obtained
- Special treatment for key components
- Wide Data Bank of binary parameters
Peng-Robinson
The Peng-Robinson equation was developed in 1976 to accomplish the following objectives:
- The parameters had to be extrapolated with respect to the acentric factor and the critical properties
- The model should be reasonably accurate close to the critical point, particularly for calculations of compressibility factor and the liquid density
- The mixing rules should not employ more than a parameter regarding the binary interactions that should be independent of pressure, temperature, and composition
- The equation should be applicable for all the calculations of all the properties of the fluids in processes involving the use of natural gas
Generally the Peng-Robinson equation provides results similar to those of the Soave equation, although it is better to predict the densities of many components in the liquid phase, especially those that are nonpolar.
The previously mentioned model is presented as follows:
The advantages of using this model in a simulation package are:
- It is the most developed model in Aspen Hysys
- High precision in a wide range of temperature and pressure
- Special treatment for key components
- Wide Data Bank of binary parameters
Note that the factors a,b and are similar to those proposed by Soave-Redlich-Kwong (SRK), but correcting the constants to improve its precision.
Prioritizing the Need to Improve Thermodynamic Model Accuracy
After a base case simulation is complete, the subject of thermodynamic model selection should be revisited in addition to a host of other process specifications designed to optimize the overall process. Changes in thermodynamic model selection will generally have a greater impact on simulation accuracy then they will on process economics.
The following additional heuristics will provide guidance as to the priority that should be placed on improving the thermodynamic model accuracy:
- Use the activity coefficient as a guide to determine the impact of the thermodynamic model on simulation accuracy. If the infinite dilution activity coefficients are all less than 1.3 and no azeotropes are encountered, it is likely that any of a number of thermodynamic models will model the system with reasonable accuracy. Use a composition of 0.1% to determine infinite dilution activity coefficients if values are not available as extrapolated to zero composition. If an EOS is used to model liquid phases, convert the partial molar fugacity coefficients to activity coefficients to apply this approach.
- If the infinite dilution activity coefficients are greater than 1.3, literature research or experimental investigation may be necessary to get improved data. The following should be considered:
- a) if the simulation package has binary interaction coefficients in its database these interaction coefficients may be suitable (check out any references for the binary interaction coefficients that may be available with the simulator to see if the conditions used to estimate the coefficients are similar to the conditions in the simulation) and
- b) conduct a sensitivity analysis using the simulator to determine how sensitive the actual design and economics are to the binary interaction coefficients and respective activity coefficients.
Both options can be used to present a case for not expending time performing a literature search or money obtaining experimental data.
Heuristic 1 is based on the fact that solution models are more accurately described not as models for estimating activity coefficients, but rather, as models for estimating how activity coefficients deviate from the ideal case of the activity coefficient being equal to 1.0. And so, if a solution model estimates an activity coefficient of 1.1 it is more accurately described as estimating an activity coefficient variation of +0.1 from the ideal case of 1.0.
Example
Consider the case of 0.1 mole fraction of water in two unspecified organics at a temperature of 100 C (Psat = 1 bar). In one case, the activity coefficient is 1.1 while in the other case the activity coefficient is 2.0.
If in each case, the correction estimated by the activity coefficient has an error of 50%. This translates to the actual partial pressures potentially ranging from 0.105 to 0.115 bar for the first case and 0.15 to 0.25 bar for the second case. The implications of a 0.01 bar uncertainty in the partial pressure are far less than the uncertainty of 0.1 bar in partial pressure.
Hence, the simple but effective heuristic 8 provides a useful guide as to the need to expend additional time in defining thermodynamic models. The value of 1.3 as a decision point is justified; however, the range of values from about 1.2 to 2.0 could be considered a transitory range where values less than 1.2 would have very little error while values greater than 2.0 could easily have considerable error.
When a system exhibits LLE, infinite dilution activity coefficients are typically >7.0. In such instances even small errors in the activity coefficients may lead to inaccurate prediction of the existence of LLE or the compositions of the LLE. For these applications, a sensitivity analysis can provide insight into how a typical solution model inaccuracy would impact process designs.
Conclusions
Thermodynamic modeling including the selection of the best models for use with process simulation is a recognized topic is chemical engineering that is held in the same regard as process simulation. However, richness and complexity of the phase equilibrium topic should not prevent engineers from using heuristics as a starting point for tapping into the ability of powerful simulation packages.
References
- G.P. Towler, R. Sinnott. Chemical Engineering Design: Principles, Practice and Economics of Plant and Process Design. Elsevier, 2012.
- I.D.G Chaves. Process Dynamcis and Simulation in Chemical Engineering. Springer, 2015.
- G.D. Ulrich, A Guide to Chemical Engineering Process Design and Economics. Wiley: New York, 1984.
- Walas, S.M.. (1990). Chemical Process Equipment - Selection and Design. Elsevier